
����Ŀ�����˶���������Ѷ������һ�����ƼƲ����ݿ�Ĺ����˺�.�û�����ͨ����ע���˶����ںŲ鿴�Լ�ÿ���ÿ�����ߵIJ�����ͬʱҲ���Ժ������û������˶�����![]() �����.�������˶���Ϊ�����Լ��IJ��������������ѣ������˶��Ļ�����������ǿ��������ij��2018��1����2018��11���ڼ�ÿ���ܲ���ƽ����̣���λ��ʮ��������ݣ����������������ͼ.
�����.�������˶���Ϊ�����Լ��IJ��������������ѣ������˶��Ļ�����������ǿ��������ij��2018��1����2018��11���ڼ�ÿ���ܲ���ƽ����̣���λ��ʮ��������ݣ����������������ͼ.
��������ͼ�����н�����ȷ���ǣ� ��
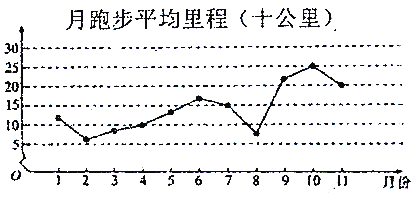
A. ���ܲ�ƽ����̵���λ��Ϊ![]() �·ݶ�Ӧ�������
�·ݶ�Ӧ�������
B. ���ܲ�ƽ�������������
C. ���ܲ�ƽ����̸߷��ڴ�����![]() ��
��![]() ��
��
D. ![]() ����
����![]() �µ����ܲ�ƽ����������
�µ����ܲ�ƽ����������![]() ����
����![]() �£������Ը�С���仯�Ƚ�ƽ��
�£������Ը�С���仯�Ƚ�ƽ��
 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ������
������![]() ��
�� ![]() ����Բ��
����Բ��![]() ��ֱ��
��ֱ��![]() ����
����
������Բ![]() �ı����̣�
�ı����̣�
����ֱ��![]() ����
����![]() ����Բ
����Բ![]() ��������ͬ�Ľ���
��������ͬ�Ľ���![]() ��
�� ![]() ����ֱ��
����ֱ��![]() ��б��
���![]() ����0����
����0����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�����ڣ��������£��Ƿ����ֱ��![]() ʹ����
ʹ����![]() �Ĵ�ֱƽ���߹���
�Ĵ�ֱƽ���߹���![]() �������ڣ����ֱ��
�������ڣ����ֱ��![]() �ķ��̣��������ڣ���˵�����ɣ�
�ķ��̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �DZ߳�Ϊ2�����Σ�
�DZ߳�Ϊ2�����Σ�![]() ��
��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ����
����![]() ��
Ϊ��![]() ���е㣮
���е㣮

��������![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
���������![]() ������ֵΪ
������ֵΪ![]() ʱ����ֱ��
ʱ����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽǣ�
���ɵĽǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ֱ��
��ֱ��![]() ��
��![]() .
.
������![]() ��
��![]() ͼ����һ�㣬
ͼ����һ�㣬![]() Ϊԭ�㣬ֱ��
Ϊԭ�㣬ֱ��![]() ��б��
���![]() ����
����![]() ��
��![]()
![]() �ϴ��ڼ�ֵ����
�ϴ��ڼ�ֵ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�����Ƿ����ʵ��![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ������
������![]() �����ߣ������ڣ����
�����ߣ������ڣ����![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
������ȷ������![]() ��ֱ��
��ֱ��![]() �Ľ����������˵������.
�Ľ����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��{bn}���㣺a1��3����n��2ʱ��an��1+an��4n�����������������n��![]() ����{bn}��ǰn���ΪSn��
����{bn}��ǰn���ΪSn��
��1��������{an}��{bn}��ͨ�ʽ��
��2��������13��Sn��14��n�ļ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��ABCD��,ƽ��![]() ��ֱ�ڶԽ���AC,��ƽ��
��ֱ�ڶԽ���AC,��ƽ��![]() �ص����������������õ�����������,�Ǵ˽��������ε����ΪS,�ܳ�Ϊl,�� ��
�ص����������������õ�����������,�Ǵ˽��������ε����ΪS,�ܳ�Ϊl,�� ��
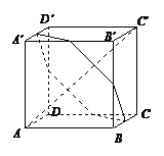
A. SΪ��ֵ,l��Ϊ��ֵ B. S��Ϊ��ֵ,lΪ��ֵ
C. S��l��Ϊ��ֵ D. S��l����Ϊ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD�DZ߳�Ϊ1�������Σ�PB��BC��PD��DC����PC![]() ��
��
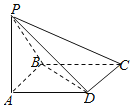
��1����֤��PA��ƽ��ABCD��
��2��������ֱ��AC��PD���ɽǵ�����ֵ��
��3��������B��PD��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A,B,C,D��ֱ������ϵ�в�ͬ���ĵ㣬��![]() ��
��![]() ����
����![]() ��������˵����ȷ����( ),
��������˵����ȷ����( ),
A.C�������߶�AB���е�
B.D�������߶�AB���е�
C.C��D����ͬʱ���߶�AB��
D.C��D������ͬʱ���߶�AB���ӳ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������![]() ��
��![]() �ϴ���
�ϴ���![]() ����
����![]() ��
��![]() ����ƺ���
����ƺ���![]() ����
����![]() �ϵġ�˫��ֵ����������֪����
�ϵġ�˫��ֵ����������֪����![]() ��
��![]() �ϵġ�˫��ֵ������������
�ϵġ�˫��ֵ������������![]() ��ȡֵ��Χ��__________��
��ȡֵ��Χ��__________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com