
(1)求点B的坐标;
(2)若直线l与双曲线C:![]() -y2=1(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
-y2=1(a>0)相交于E、F两点,且线段EF的中点坐标为(4,1),求a的值;
(3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的距离h关于t的函数关系式.
解:(1)直线AB的方程为y=x-3.
设B(x,y),由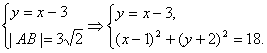
由x>0,y>0得![]()
∴点B的坐标为(4,1).
(2)由方程组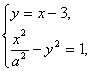 得(
得(![]() -1)x2+6x-10=0.
-1)x2+6x-10=0.
设两个交点分别为E(x1,y1)、F(x2,y2),
则x1+x2=-![]() .
.
又∵EF的中点坐标为(4,1),则![]() =4.
=4.
∴![]() =4,即得a=2.
=4,即得a=2.
(3)设线段AB上任一点Q的坐标为(x,x-3)(1≤x≤4).
则|PQ|=![]() .
.
令f(x)=![]() =
=![]() (1≤x≤4).
(1≤x≤4).
①当1≤![]() ≤4,即-1≤t≤5时,
≤4,即-1≤t≤5时,
|PQ|min=f(![]() )=
)=![]() ;
;
②当![]() >4,即t>5时,f(x)在[1,4]上单调递减,
>4,即t>5时,f(x)在[1,4]上单调递减,
∴|PQ|min=f(4)=![]() ;
;
③当![]() <1,即t<-1时,f(x)在[1,4]上单调递增,
<1,即t<-1时,f(x)在[1,4]上单调递增,
∴|PQ|min=f(1)=![]() .
.
综上所述,
h(t)=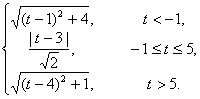


科目:高中数学 来源: 题型:
| 2 |
| x2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源:苏州模拟 题型:解答题
| 2 |
| x2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求点B的坐标;
(2)若直线l与双曲线C:![]() -y2=1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值;
-y2=1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值;
(3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P 与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的 距离h关于t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com