
分析 用单调性定义来证明,先在给定区间上取两个变量,且界定大小,不妨设x1<x2<0则有-x1>-x2>0,再由“f(x)在(0,+∞)上是减函数”可得到f(-x1)>f(-x2),然后由“f(x)是偶函数”转化为f(x1)<f(x2),再由单调性定义判断.
解答 解:f(x)在(-∞,0)上是增函数(1分)
证明:设x1<x2<0则-x1>-x2>0(3分)
∵f(x)在(0,+∞)上是减函数
∴f(-x1)<f(-x2)(7分)
又f(x)是偶函数
∴f(-x1)=f(x1),f(-x2)=f(x2)
∴f(x1)<f(x2)
∴f(x)在(-∞,0)上是增函数(12分)
点评 本题主要考查奇偶函数在对称区间上的单调性,结论是:偶函数在对称区间上的单调性相反,奇函数在对称区间上的单调性相同.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
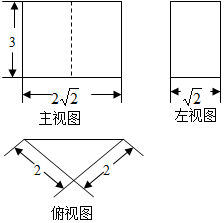
| A. | $(16+6\sqrt{2})c{{m}^{2}}^{\;}$ | B. | 22cm2 | C. | $(12+6\sqrt{2})c{m}^{2}$ | D. | $(18+2\sqrt{3})c{m}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆锥的顶点与底面圆周上的任意一点的连线都是母线 | |
| B. | 以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥 | |
| C. | 棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥 | |
| D. | 各个面都是三角形的几何体是三棱锥 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $-\frac{5}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|-2<x<2} | C. | {x|0<x<1} | D. | {x|1<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com