
【题目】已知数列{an}满足条件(n﹣1)an+1=(n+1)(an﹣1),且a2=6,
(1)计算a1、a3、a4 , 请猜测数列{an}的通项公式并用数学归纳法证明;
(2)设bn=an+n(n∈N*),求 ![]() 的值.
的值.
【答案】
(1)解:当n=1时,a1=1,且a2=6
当n=2时,a3=3(a2﹣1)=15,
当n=3时,2a4=4(a3﹣1),∴a4=28,
猜测 ![]()
下面用数学归纳法证明:
ⅰ当n=1,2,3,4时,等式 ![]() 已成立
已成立
ⅱ假设当n=k时, ![]()
则由(k﹣1)ak+1=(k+1)(ak﹣1),有: ![]() =2k2+3k+1=2(k+1)2﹣(k+1)
=2k2+3k+1=2(k+1)2﹣(k+1)
即n=k+1时,等式也成立
综上, ![]() 成立
成立
(2)解:bn=an+n=2n2
∴bn﹣2=2(n﹣1)(n+1)
∴ ![]() =
= ![]() (
( ![]() )
)
∴ ![]() =
= ![]()
= ![]() =
= ![]()
【解析】(1)计算前几项,猜想数列的通项,再利用数学归纳法进行证明;(2)确定数列的通项,利用裂项法求和,即可求得结论.
【考点精析】利用数学归纳法的定义对题目进行判断即可得到答案,需要熟知数学归纳法是证明关于正整数n的命题的一种方法.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线![]() .(1)求曲线
.(1)求曲线![]() 的普通方程;(2)若点
的普通方程;(2)若点![]() 在曲线
在曲线![]() 上,点
上,点![]()
![]() ,当点
,当点![]() 在曲线
在曲线![]() 上运动时,求
上运动时,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c且b=c,∠A的平分线为AD,若 ![]() =m
=m ![]()
![]() .
.
(1)当m=2时,求cosA
(2)当 ![]() ∈(1,
∈(1, ![]() )时,求实数m的取值范围.
)时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项为正的数列{an}是等比数列,a1=2,a5=32,数列{bn}满足:对于任意n∈N* , 有a1b1+a2b2+…+anbn=(n﹣1)2n+1+2.
(1)求数列{an}的通项公式;
(2)令f(n)=a2+a4+…+a2n , 求 ![]() 的值;
的值;
(3)求数列{bn}通项公式,若在数列{an}的任意相邻两项ak与ak+1之间插入bk(k∈N*)后,得到一个新的数列{cn},求数列{cn}的前100项之和T100 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个定义域相同的函数f(x),g(x),若存在实数m、n使h(x)=mf(x)+ng(x),则称函数h(x)是由“基函数f(x),g(x)”生成的.
(1)若f(x)=x2+3x和个g(x)=3x+4生成一个偶函数h(x),求h(2)的值;
(2)若h(x)=2x2+3x﹣1由函数f(x)=x2+ax,g(x)=x+b(a、b∈R且ab≠0)生成,求a+2b的取值范围;
(3)利用“基函数f(x)=log4(4x+1),g(x)=x﹣1”生成一个函数h(x),使之满足下列件:①是偶函数;②有最小值1;求函数h(x)的解析式并进一步研究该函数的单调性(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的实数满足:f(x+3)=﹣ ![]() ,且当﹣3≤x<﹣1时,f(x)=﹣(x+2)2 , 当﹣1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2016)= .
,且当﹣3≤x<﹣1时,f(x)=﹣(x+2)2 , 当﹣1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2016)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且 ![]() ,∠AOQ=α,α∈[0,π). (Ⅰ)若点Q的坐标是
,∠AOQ=α,α∈[0,π). (Ⅰ)若点Q的坐标是 ![]() ,求
,求 ![]() 的值;
的值;
(Ⅱ)设函数 ![]() ,求f(α)的值域.
,求f(α)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC= ![]() BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点.
BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点. 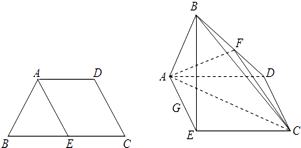
(1)求三棱锥E﹣ACB1的体积;
(2)证明:B1E∥平面ACF;
(3)证明:平面B1GD⊥平面B1DC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com