
【题目】已知函数![]() ,其中
,其中![]() 为实常数.
为实常数.
(1)若当![]() 时,
时,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)对任意不同两点![]() ,
,![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)![]() 讨论
讨论![]() 与0,1,e的大小关系确定最值得a的方程即可求解;(2)原不等式化为
与0,1,e的大小关系确定最值得a的方程即可求解;(2)原不等式化为![]() ,不妨设
,不妨设![]() ,整理得
,整理得![]() ,设
,设![]() ,当
,当![]() 时,
时,![]() ,得
,得![]() ,分离
,分离![]() ,求其最值即可求解a的范围
,求其最值即可求解a的范围
(1)![]() ,令
,令![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
①当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,
由已知,![]() ,即
,即![]() ,符合题意.
,符合题意.
②当![]() 时,即
时,即![]() 时,
时,![]() 在区间上单调递增,在上单调递减,
在区间上单调递增,在上单调递减,
则![]() ,由已知,
,由已知,![]() ,即
,即![]() ,不符合题意,舍去.
,不符合题意,舍去.
③当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,则,
上单调递增,则,
由已知,![]() ,即
,即![]() ,不符合题意,舍去.
,不符合题意,舍去.
综上分析,![]() .
.
(2)由题意,![]() ,则原不等式化为
,则原不等式化为![]() ,
,
不妨设![]() ,则
,则![]() ,即
,即![]() ,
,
即![]() .
.
设![]() ,则
,则![]() ,
,
由已知,当![]() 时,不等式
时,不等式![]() 恒成立,则
恒成立,则![]() 在
在![]() 上是增函数.
上是增函数.
所以当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() 恒成立,
恒成立,
因为![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,所以
时取等号,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
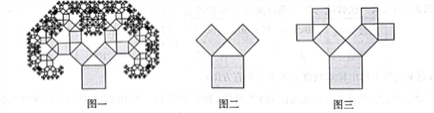
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过对本地养鱼场年利润率的调研,其结果是:年利润亏损10%的概率为0.2,年利润获利30%的概率为0.4,年利润获利50%的概率为0.4,对远洋捕捞队的调研结果是:年利润获利为60%的概率为0.7,持平的概率为0.2,年利润亏损20%的可能性为0.1. 为确保本地的鲜鱼供应,市政府要求该公司对远洋捕捞队的投资不得高于本地养鱼场的投资的2倍.根据调研数据,该公司如何分配投资金额,明年两个项目的利润之和最大值为_________千万.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防某流感病毒,某学校对教室进行药熏消毒,室内每立方米空气中的含药量![]() (单位:毫克)随时间
(单位:毫克)随时间![]() (单位:
(单位:![]() )的变化情况如下图所示,在药物释放的过程中,
)的变化情况如下图所示,在药物释放的过程中,![]() 与
与![]() 成正比:药物释放完毕后,
成正比:药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为 (
(![]() 为常数),根据图中提供的信息,回答下列问题:
为常数),根据图中提供的信息,回答下列问题:

(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室学习,那么从药物释放开始,至少需要经过多少小时后,学生才能回到教空?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解日益拥堵的交通状况,不少城市实施车牌竞价策略,以控制车辆数量.某地车牌竞价的基本规则是:①“盲拍”,即所有参与竞拍的人都要网络报价一次,每个人不知晓其他人的报价,也不知道参与当期竞拍的总人数;②竞价时间截止后,系统根据当期车牌配额,按照竞拍人的出价从高到低分配名额.某人拟参加2018年5月份的车牌竞拍,他为了预测最低成交价,根据竞拍网站的数据,统计了最近5个月参与竞拍的人数(见下表):

(1)由收集数据的散点图发现,可用线性回归模型拟合竞拍人数y(万人)与月份编号t之间的相关关系.请用最小二乘法求y关于t的线性回归方程:![]() ,并预测2018年5月份参与竞拍的人数.
,并预测2018年5月份参与竞拍的人数.
(2)某市场调研机构从拟参加2018年5月份车牌竞拍人员中,随机抽取了200人,对他们的拟报价价格进行了调查,得到如下频数分布表和频率分布直方图:


(i)求![]() 的值及这200位竟拍人员中报价大于5万元的人数;
的值及这200位竟拍人员中报价大于5万元的人数;
(ii)若2018年5月份车牌配额数量为3000,假设竞拍报价在各区间分布是均匀的,请你根据以上抽样的数据信息,预测(需说明理由)竞拍的最低成交价.
参考公式及数据:①![]() ,其中
,其中 ;
;
②![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() ,周长为6.
,周长为6.
(1)求椭圆![]() 的方程,并求椭圆
的方程,并求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若在
,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 与
与![]() 中点的连线与直线
中点的连线与直线![]() 垂直,求实数
垂直,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com