

 ,根据直径所对的圆周角是直角,得
,根据直径所对的圆周角是直角,得 ,根据等量代换得
,根据等量代换得 ,最后利用三角形的性质即可得出
,最后利用三角形的性质即可得出 ,从而得到
,从而得到 ;
; ,根据
,根据 ,得到
,得到 ,再由(1)知,
,再由(1)知, ,等量代换得
,等量代换得 ,即
,即 即可证出结论.此题比较基础,属于基础题型,平时多加练习,能够拿满分.
即可证出结论.此题比较基础,属于基础题型,平时多加练习,能够拿满分.

科目:高中数学 来源:不详 题型:解答题
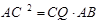
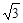 ,BP=2,求QD.
,BP=2,求QD.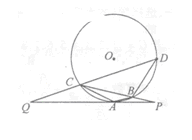
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.2∶1 | B.1∶1 |
| C.1∶2 | D.1∶1.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com