解:(1)由
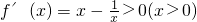
得,x>1,
故f(x)在(1,+∞)递增,在(0,1)递减,
故f(x)有极小值为

,无极大值.
(2)由g'(x)=-(x
2-3x+1)e
x-(2x-3)e
x=-(x
2-x-2)e
x>0得,
解得0<x<2
故g(x)在(0,2)递增,在(2,+∞)递减,
故g(x)
max=g(2)=e
2-9<0
又由(1)知
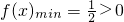
,
故不存在x
0满足条件.
(3)问题转化为f(x)的最小值大于g(x)+a的最大值,
由(2)得,
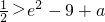
,
故

分析:(1)求出f(x)的导数,令导数大于0,求出x的范围即函数的单调递增区间,进一步求出单调递减求出,根据极值的大于得到极值.
(2)求出g(x)的导数,令导函数大于0,求出函数的单调递增区间,进一步求出单调递减区间,求出g(x)的最大值,判断出f(x)的最小值与g(x)的最大值的特殊关系,得到不存在x
0满足条件.
(3)将不等式恒成立问题转化为(x)的最小值大于g(x)+a的最大值,将(1),(2)中求出的最值代入,得到关于a的不等式,解不等式求出a 的范围.
点评:求函数的单调区间,一般求出函数的导函数,令导函数大于0求出单调递增区间,令导函数小于0求出函数的单调递减区间;解决不等式恒成立问题,常转化为函数的最值问题.

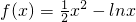 ,g(x)=-(x2-3x+1)ex-9(x>0).
,g(x)=-(x2-3x+1)ex-9(x>0).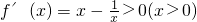
 ,无极大值.
,无极大值. 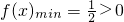 ,
,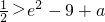 ,
,

