
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)设![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,存在
,存在![]() 使
使![]() ,求实数
,求实数![]() 取值.
取值.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;函数
上单调递减;函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;函数
上单调递减;函数![]() 在
在![]() 上单调递增;函数
上单调递增;函数![]() 在
在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】分析:(1)先求定义域,再对函数求导,![]()
![]() ,
,
令![]()
![]() ,分
,分![]() ,
,![]() ,
,![]() ,
,![]() ,四种情况考虑h(x)零点情况及正负情况,得函数f(x)的单调区间。
,四种情况考虑h(x)零点情况及正负情况,得函数f(x)的单调区间。
(2)因为![]() ,由于(I)知,
,由于(I)知,![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
由题意可知“对任意![]() ,存在
,存在![]() ,使
,使![]() ”等价于“
”等价于“![]() 在
在![]() 上的最小值不大于
上的最小值不大于![]() 在
在![]() 上的最小值
上的最小值![]() ”,由一元二次函数的“三点一轴”分类讨论求得g(x)的最小值,再求得b范围。
”,由一元二次函数的“三点一轴”分类讨论求得g(x)的最小值,再求得b范围。
详解:(1)定义域![]()
因为![]()
所以![]()
![]()
![]()
令![]()
![]()
(i)当![]() 时,
时, ![]()
![]()
所以当![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递增
单调递增
(ii)当![]() 时,由
时,由![]() ,
,
即![]() ,解得
,解得![]()
①当![]() 时,
时, ![]() ,
,![]() 恒成立,此时
恒成立,此时![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
②当![]() 时,
时, ![]()
![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递增;
单调递增;
![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递减;
单调递减;
③当![]() 时,由于
时,由于![]()
![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 单调递增;
单调递增;
综上所述:
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
函数![]() 在
在![]() 上单调递增;
上单调递增;
函数![]() 在
在![]() 上单调递减
上单调递减
(2)因为![]() ,由于(I)知,
,由于(I)知, ![]() ,当
,当![]() 时,
时, ![]() ,
,
函数![]() 单调递减:当
单调递减:当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 上的最小值为
上的最小值为![]()
由于“对任意![]() ,存在
,存在![]() ,使
,使![]() ”等价于“
”等价于“![]() 在
在![]() 上的最小值不大于
上的最小值不大于![]() 在
在![]() 上的最小值
上的最小值![]() ”
”
又![]() ,
,![]() ,所以
,所以
①当![]() 时,因为
时,因为![]()
![]() ,此时与
,此时与![]() 矛盾
矛盾
②当![]() 时,因为
时,因为![]() ,同样与
,同样与![]() 矛盾
矛盾
③当![]() 时,因为
时,因为![]() ,解不等式
,解不等式![]()
可得![]()
综上, ![]() 的取值范围是
的取值范围是![]() .
.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司制造两种电子设备:影片播放器和音乐播放器.在每天生产结束后,要对产品进行检测,故障的播放器会被移除进行修复. 下表显示各播放器每天制造的平均数量以及平均故障率.
商品类型 | 播放器每天平均产量 | 播放器每天平均故障率 |
影片播放器 | 3000 | 4% |
音乐播放器 | 9000 | 3% |
下面是关于公司每天生产量的叙述:
①每天生产的播放器有三分之一是影片播放器;
②在任何一批数量为100的影片播放器中,恰好有4个会是故障的;
③如果从每天生产的音乐播放器中随机选取一个进行检测,此产品需要进行修复的概率是0.03.
上面叙述正确的是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)已知函数f(x)=|2x﹣3|﹣2|x|,若关于x不等式f(x)≤|a+2|+2a恒成立,求实数a的取值范围; (Ⅱ)已知正数x,y,z满足2x+y+z=1,求证 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为假命题:
”的逆否命题为假命题:
②命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
③若“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,则
”为假命题,则![]() 为真命题,
为真命题,![]() 为假命题;
为假命题;
④函数![]() 有极值的充要条件是
有极值的充要条件是![]() 或
或![]() .
.
其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e2x(ax2+2x﹣1),a∈R.
(Ⅰ)当a=4时,求证:过点P(1,0)有三条直线与曲线y=f(x)相切;
(Ⅱ)当x≤0时,f(x)+1≥0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
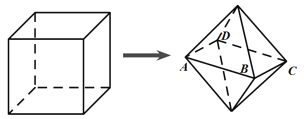
【题目】如图,棱长为1(单位:![]() )的正方体木块经过适当切割,得到几何体
)的正方体木块经过适当切割,得到几何体![]() ,已知几何体
,已知几何体![]() 由两个底面相同的正四棱锥组成,底面
由两个底面相同的正四棱锥组成,底面![]() 平行于正方体的下底面,且各顶点均在正方体的面上,则几何体
平行于正方体的下底面,且各顶点均在正方体的面上,则几何体![]() 体积的取值范围是________(单位:
体积的取值范围是________(单位:![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生参加了“铅球”和“立定跳远”两个科目的体能测试,每个科目的成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级,分别对应5分,4分,3分,2分,1分,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为
五个等级,分别对应5分,4分,3分,2分,1分,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为![]() 的学生有8人.
的学生有8人.

(Ⅰ)求该班学生中“立定跳远”科目中成绩为![]() 的人数;
的人数;
(Ⅱ)若该班共有10人的两科成绩得分之和大于7分,其中有2人10分,3人9分,5人8分.从这10人中随机抽取两人,求两人成绩之和![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在xOy平面上,将双曲线的一支![]()
![]() 及其渐近线
及其渐近线![]() 和直线
和直线![]() 、
、![]() 围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周所得的几何体为
围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周所得的几何体为![]() ,过
,过![]()
![]() 作
作![]() 的水平截面,计算截面面积,利用祖暅原理得出
的水平截面,计算截面面积,利用祖暅原理得出![]() 体积为________
体积为________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com