
【题目】已知![]() .
.
(1)当![]() =-1时,求
=-1时,求![]() 的单调区间及值域;
的单调区间及值域;
(2)若![]() 在(
在(![]() )上为增函数,求实数
)上为增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)f(x)的值域为(-∞,2-log23].增区间为![]() ,减区间为
,减区间为![]() .(2)
.(2)![]()
【解析】
(1) 当a=-1时,f(x)=log![]() (x2+x+1),log
(x2+x+1),log![]() (x2+x+1)≤log
(x2+x+1)≤log![]()
![]() =2-log23,
=2-log23,
∴f(x)的值域为(-∞,2-log23].由对数式的真数大于0求得函数的定义域,得到内函数的单调区间,结合复合函数的单调性得答案.
(2)用复合函数的单调性来求解,令u(x)=x2-ax-a=![]() 2-
2-![]() -a,
-a,
由“若f(x)在![]() 上为增函数,”,可知u(x)应在
上为增函数,”,可知u(x)应在![]() 上为减函数且
上为减函数且
u(x)>0在![]() 恒成立.再用“对称轴在区间的右侧,且最小值大于零”求解可得结果.
恒成立.再用“对称轴在区间的右侧,且最小值大于零”求解可得结果.
解 (1)当a=-1时,f(x)=log![]() (x2+x+1),
(x2+x+1),
∵x2+x+1=![]() 2+
2+![]() ≥
≥![]() ,
,
∴log![]() (x2+x+1)≤log
(x2+x+1)≤log![]()
![]() =2-log23,
=2-log23,
∴f(x)的值域为(-∞,2-log23].
∵y=x2+x+1在![]() 上递减,在
上递减,在![]() 上递增,y=log
上递增,y=log![]() x在(0,+∞)上递减,
x在(0,+∞)上递减,
∴f(x)的增区间为![]() ,
,
减区间为![]() .
.
(2)令u(x)=x2-ax-a=![]() 2-
2-![]() -a,
-a,
∵f(x)在![]() 上为单调增函数,
上为单调增函数,
又∵y=log![]() u(x)为单调减函数,
u(x)为单调减函数,
∴u(x)在![]() 上为单调减函数,且u(x)>0在
上为单调减函数,且u(x)>0在![]() 上恒成立.
上恒成立.![]()
因此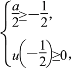 即
即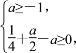
解得-1≤a≤![]() .
.
故实数a的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 为参数),P、Q分别为直线
为参数),P、Q分别为直线![]() 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =![]() ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = ![]() ,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.

(1)若以F、B、C、D为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;
的最大值;
(2)当 ![]() 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】片森林原来面积为a,计划每年砍伐森林面积是上一年末森林面积的p%,当砍伐到原来面积的一半时,所用时间是10年,已知到今年末为止,森林剩余面积为原来面积的![]() ,为保护生态环境,森林面积至少要保留原来面积的
,为保护生态环境,森林面积至少要保留原来面积的![]() .
.
(1)求每年砍伐面积的百分比p%;
(2)到今年为止,该森林已砍伐了多少年?
(3)今年以后至多还能再砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
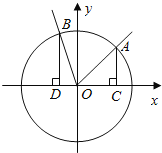
【题目】如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且![]() .将角α的终边按逆时针方向旋转
.将角α的终边按逆时针方向旋转![]() ,交单位圆于点B.记A(x1,y1),B(x2,y2).
,交单位圆于点B.记A(x1,y1),B(x2,y2).
(Ⅰ)若![]() ,求x2;
,求x2;
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=2S2,求角α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com