Question

【题目】已知函数，且在处的切线与平行．

求的单调区间；

若存在区间，使在上的值域是，求b的取值范围．

Answer 1

【答案】(1)见解析.

【解析】

对函数求导，由求出a的值，然后将a的值代入导数，求出极值点，讨论导数的正负，即可求出函数的单调区间；由函数在区间上单调递增得到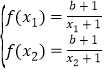，将问题转化为关于x的方程在区间上有两个解，利用参变量分离法得出在区间上有两个解，构造函数，利用导数研究函数的单调性与极值，作出函数在区间上的图象，即可求出b的取值范围．

由，得，

由，得．

．

则，

由，得，由，得．

的单调减区间为，增区间为；

由知，，且函数在区间上单调递增，若存在区间，使在上的值域是，

则有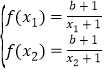，则，得，

所以，关于x的方程在区间上有两解，

由，得，构造函数，其中，

所以，直线与函数的图象在区间上有两个交点，

，

构造函数，则，

所以，函数在区间上单调递增，由于，

当时，，即；当时，，即．

所以，函数在区间上单调递减，在区间上单调递增，

所以，函数在处取得最小值，即，

由于，，所以，，

结合图象可知，当时，直线与函数在区间上的图象有两个交点，

因此，实数b的取值范围是．