Question

已知盘中有编号为A，B，C，D的4个红球，4个黄球，4个白球（共 12个球）现从中摸出4个球（除编号与颜色外球没有区别）
（I）求恰好包含字母A，B，C，D的概率；
（II）设摸出的4个球中出现的颜色种数为随机变量X．求X的分布列和期望E（X）．

Answer 1

解：（Ⅰ）记事件“恰好包含字母A，B，C，D”为E，
则P（E）=．（5分）
（Ⅱ） 由题意可得随机变量X的取值可能为：1，2，3，且，
，．
故X的分布列为：

X	1	2	3
P

（12分）
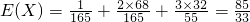
故数学期望为．（14分）
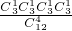
分析：（Ⅰ）记事件“恰好包含字母A，B，C，D”为E，则P（E）=，计算即可；（Ⅱ） 由题意可得随机变量X的取值可能为：1，2，3，分别求其概率，可得分布列为，进而可得数学期望．
点评：本题考查离散型随机变量的分布列及数学期望，属中档题．