练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知四边形为正方形，平面，四边形与四边形也都为正方形，连接，点为的中点，有下述四个结论：

    ①； 　　　　②与所成角为；　　　　

    ③平面； 　　　　④与平面所成角为．

    其中所有正确结论的编号是（ ）

    A.①②B.①②③C.①③④D.①②③④

    【答案】B

    【解析】

    根据题意建立空间直角坐标系，写出所有点的坐标，利用向量法可以判断出正确的结论.

    由题意得，所得几何体可以看成一个正方体，

    因此所在直线分别为轴，建立空间直角坐标系，

    设，

    ，，，，，

    ，，，

    ①，，

    ，

    ，，①是正确的.

    ②，，

    设与所成的角为，

    ，

    ，②是正确的.

    ③，，，

    设是平面的一个法向量，

    ，

    取，，

    ，，

    平面，③是正确.

    ④，由图像易得：是平面的一个法量，

    设与平面所成的角为，

    ，

    ，

    ，④不正确，

    综上：①②③正确.

    故选：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆长轴长为短轴长的两倍，连结椭圆的四个顶点得到的菱形的面积为4，直线过点，且与椭圆相交于另一点.

    （1）求椭圆的方程；

    （2）若线段长为，求直线的倾斜角；

    （3）点在线段的垂直平分线上，且，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】实数a，b满足ab＞0且a≠b，由a、b、、按一定顺序构成的数列（　　）

    A. 可能是等差数列，也可能是等比数列

    B. 可能是等差数列，但不可能是等比数列

    C. 不可能是等差数列，但可能是等比数列

    D. 不可能是等差数列，也不可能是等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：

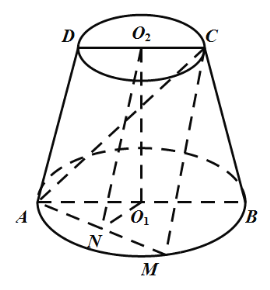
    【题目】如图，在圆台中，平面过上下底面的圆心，，点M在上，N为的中点，.

    （1）求证：平面平面；

    （2）当时，与底面所成角的正弦值为，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知非空集合是由一些函数组成，满足如下性质：①对任意，均存在反函数，且；②对任意，方程均有解；③对任意、，若函数为定义在上的一次函数，则.

    （1）若，，均在集合中，求证：函数；

    （2）若函数（）在集合中，求实数的取值范围；

    （3）若集合中的函数均为定义在上的一次函数，求证：存在一个实数，使得对一切，均有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

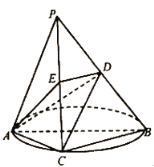
    【题目】如图，是一个三棱锥，是圆的直径，是圆上的点，垂直圆所在的平面，，分别是棱，的中点.

    （1）求证：平面；

    （2）若二面角是，，求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 已知抛物线的顶点为坐标原点，焦点在轴的正半轴上，过点的直线与抛物线相交于，两点，且满足

    （1）求抛物线的方程；

    （2）若是抛物线上的动点，点在轴上，圆内切于，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义域为R的函数，若函数是奇函数，则称为正弦奇函数.已知 是单调递增的正弦奇函数，其值域为R，.

    （1）已知是正弦奇函数，证明：“为方程的解”的充要条件是“为方程的解”；

    （2）若，求的值；

    （3）证明：是奇函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在圆上任取一点，过点作轴的垂线段，为垂足，当点在圆上运动时，点在线段上，且，点的轨迹为曲线.

    （1）求曲线的方程；

    （2）过抛物线：的焦点作直线交抛物线于，两点，过且与直线垂直的直线交曲线于另一点，求面积的最小值，以及取得最小值时直线的方程.

    查看答案和解析>>

    同步练习册答案