
【题目】设函数![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 内存在唯一极值点
内存在唯一极值点![]() ,求实数
,求实数![]() 的取值范围,并判断
的取值范围,并判断![]() 是
是![]() 在
在![]() 内的极大值点还是极小值点.
内的极大值点还是极小值点.
【答案】(1) ![]() (2)
(2) ![]() ,且
,且![]() 为函数
为函数![]() 的极小值点.
的极小值点.
【解析】
(1)先求出函数的导函数![]() ,再求出切线的斜率
,再求出切线的斜率![]() ,再由直线的点斜式方程求解即可;
,再由直线的点斜式方程求解即可;
(2)函数![]() 在
在![]() 内存在唯一极值点等价于方程
内存在唯一极值点等价于方程![]() 在
在![]() 内存在唯一解,再构造函数
内存在唯一解,再构造函数![]() ,求其值域,则可得
,求其值域,则可得![]() 的范围,再利用导数确定
的范围,再利用导数确定![]() 是极大值点或者极小值点.
是极大值点或者极小值点.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
所求切线的斜率![]() ,又
,又![]() .
.
所以曲线![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]() .
.
(2)![]() ,
,
又![]() ,则要使得
,则要使得![]() 在
在![]() 内存在唯一极值点,则
内存在唯一极值点,则![]() 在
在![]() 存在唯一变号零点,即方程
存在唯一变号零点,即方程![]() 在
在![]() 内存在唯一解,即
内存在唯一解,即![]() 与
与![]() 在
在![]() 范围内有唯一交点,
范围内有唯一交点,
设函数![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递减,又
单调递减,又![]() ;当
;当![]() 时,
时,![]()
![]() 时,
时,![]() 与
与![]() 在
在![]() 范围内有唯一交点,不妨设交点横坐标为
范围内有唯一交点,不妨设交点横坐标为![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ,
,![]() 在
在![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,则
,则![]() ,
,![]() 在
在![]() 为增函数,即
为增函数,即![]() 为函数
为函数![]() 的极小值点,
的极小值点,
综上所述:![]() ,且
,且![]() 为函数
为函数![]() 的极小值点.
的极小值点.


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为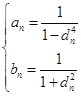 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 上放置一个边长为1的正方形
上放置一个边长为1的正方形![]() ,此正方形
,此正方形![]() 沿
沿![]() 轴滚动(向左或向右均可),滚动开始时,点
轴滚动(向左或向右均可),滚动开始时,点![]() 位于原点处,设顶点
位于原点处,设顶点![]() 的纵坐标与横坐标的函数关系式
的纵坐标与横坐标的函数关系式![]() ,
,![]() ,该函数相邻两个零点之间的距离为
,该函数相邻两个零点之间的距离为![]() .
.
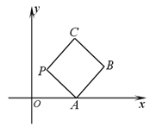
(1)写出![]() 的值并求出顶点
的值并求出顶点![]() 到
到![]() 的最小运动路径的长度
的最小运动路径的长度![]() 的值;
的值;
(2)写出函数![]() ,
,![]() ,
,![]() 的表达式;并研究该函数除周期外的基本性质(无需证明).
的表达式;并研究该函数除周期外的基本性质(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中无理数
,其中无理数![]() .
.
(Ⅰ)若函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的极值点有三个,最小的记为
的极值点有三个,最小的记为![]() ,最大的记为
,最大的记为![]() ,若
,若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (Ⅰ)求曲线
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;(Ⅱ)设直线
的直角坐标方程,并指出其表示何种曲线;(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,试求当
,试求当![]() 时,
时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】清华大学自主招生考试题中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:
题 | A | B | C |
答卷数 | 180 | 300 | 120 |
(Ⅰ)负责招生的教授为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为![]() ,求
,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com