
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系.已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(Ⅰ)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(Ⅰ)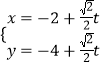 (
(![]() 为参数);(Ⅱ)
为参数);(Ⅱ)![]() .
.
【解析】试题(Ⅰ)由![]() ,
,![]() 将直线
将直线![]() 的极坐标方程化为直角坐标方程
的极坐标方程化为直角坐标方程![]() ,再由
,再由![]() ,得
,得![]() ,可得直线
,可得直线![]() 的参数方程为
的参数方程为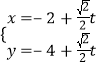 (
(![]() 为参数).(Ⅱ)先根据直线参数方程的几何意义化简条件
为参数).(Ⅱ)先根据直线参数方程的几何意义化简条件![]() 得
得![]() ,即
,即![]() ,再由
,再由![]() ,
,![]() 将曲线
将曲线![]() 的极坐标方程化为直角坐标方程
的极坐标方程化为直角坐标方程![]() (
(![]() ),并将直线参数方程代入曲线
),并将直线参数方程代入曲线![]() 的直角坐标方程,最后利用韦达定理代入条件可解得实数
的直角坐标方程,最后利用韦达定理代入条件可解得实数![]() 的值.
的值.
试题解析:(Ⅰ)将![]() ,
,![]() ,代入直线
,代入直线![]() 的极坐标方程得直角坐标方程
的极坐标方程得直角坐标方程![]() ,
,
再将![]() ,代入直线
,代入直线![]() 的直角坐标方程,得
的直角坐标方程,得![]() ,
,
所以直线![]() 的参数方程为
的参数方程为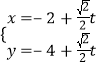 (
(![]() 为参数).
为参数).
(Ⅱ)由![]() (
(![]() ),得
),得![]() (
(![]() ),
),
由![]() ,
,![]() 代入,得
代入,得![]() (
(![]() ).
).
将直线![]() 的参数方程与
的参数方程与![]() 的直角坐标方程联立,得
的直角坐标方程联立,得![]() ,(*)
,(*)![]() .
.
设点![]() ,
,![]() 分别对应参数
分别对应参数![]() ,
,![]() 恰为上述方程的根,则
恰为上述方程的根,则![]() ,
,![]() ,
,![]() ,
,
由题设得![]() ,即
,即![]() ,
,
由(*)得![]() ,
,![]() ,
,
则有![]() ,得
,得![]() 或
或![]() ,
,
因为![]() ,所以
,所以![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】随着经济快速增长、居民收入稳步提升,消费结构逐步优化升级,生活品质显著增强,美好生活蓝图正在快速构建.某市城镇居民人均消费支出从1998年的7500元增长到2018年的40000元.1998年与2018年该市城镇居民消费结构对比如下图所示:


1988年某市城镇居民消费结构 2018年某市城镇居民消费结构
则下列叙述中不正确的是( )
A.2018年该市城镇居民人均食品支出占比同1998年相比大幅度降低
B.2018年该市城镇居民人均教育文化娱乐支出同1998年相比提高减少
C.2018年该市城镇居民人均医疗保健支出占比同1998年相比提高60%
D.2018年该市城镇居民人均交通和通信支出突破5000元,大约是1998年的14倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人用擂台赛形式进行训练.每局两人单打比赛,另一人当裁判.每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时,发现甲共打![]() 局,乙共打
局,乙共打![]() 局,而丙共当裁判
局,而丙共当裁判![]() 局.那么整个比赛的第
局.那么整个比赛的第![]() 局的输方( )
局的输方( )
A. 必是甲 B. 必是乙 C. 必是丙 D. 不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.

(1)证明:![]() ;
;
(2)是否存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
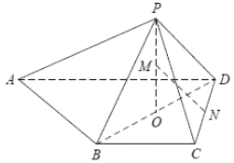
【题目】已知四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在底面
在底面![]() 上的射影是
上的射影是![]() 的中点
的中点![]() ,
,![]() .
.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)当四棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准,新标准规定,车辆驾驶人血液中的酒精含量大于或等于20毫克/百毫升、小于80毫克/百毫升的行为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝一瓶啤酒后酒精在人体血液内的变化规律“散点图”如下:

该函数模型如下,
 .
.
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时才可以驾车?(时间以整小时计)(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解市民吃肉难的生活问题,某生猪养殖公司欲将一批猪肉用冷藏汽车从甲地运往相距![]() 千米的乙地,运费为每小时
千米的乙地,运费为每小时![]() 元,装卸费为
元,装卸费为![]() 元,猪肉在运输途中的损耗费(单位:元)是汽车速
元,猪肉在运输途中的损耗费(单位:元)是汽车速![]() 度值的
度值的![]() 倍.(说明:运输的总费用=运费+装卸费+损耗费)
倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)若汽车的速度为每小时![]() 千米,试求运输的总费用;
千米,试求运输的总费用;
(2)为使运输的总费用不超过![]() 元,求汽车行驶速度的范围;
元,求汽车行驶速度的范围;
(3)若要使运输的总费用最小,汽车应以每小时多少千米的速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com