
【题目】已知集合![]() 函数
函数![]() ,函数
,函数![]() 的值域为
的值域为![]() ,
,
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 的解集
的解集![]() ,求实数
,求实数![]() 的值
的值
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,![]() 和
和![]() 都是正三角形,
都是正三角形,![]() , E、F分别是AC、BC的中点,且PD⊥AB于D.
, E、F分别是AC、BC的中点,且PD⊥AB于D.
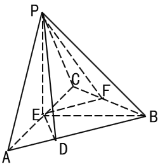
(Ⅰ)证明:直线![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为 an=(n﹣k1)(n﹣k2),其中k1,k2∈Z:
(1)试写出一组k1,k2∈Z的值,使得数列{an}中的各项均为正数;
(2)若k1=1、k2∈N*,数列{bn}满足bn=![]() ,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
(3)若0<k1<k2,数列{cn}满足cn=an+|an|,其前n项和为Sn,且使ci=cj≠0(i,j∈N*,i<j)的i和j有且仅有4组,S1、S2、…、Sn中至少3个连续项的值相等,其他项的值均不相等,求k1,k2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1的侧面AA1B1B是菱形,侧面AA1C1C是矩形,平面AA1C1C⊥平面AA1B1B,∠BAA1![]() ,AA1=2AC=2,O为AA1的中点.
,AA1=2AC=2,O为AA1的中点.
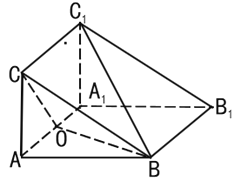
(1)求证:OC⊥BC1;
(2)求点C1到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
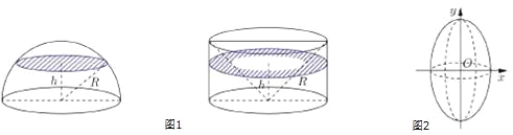
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 由方程到
由方程到![]() 确定,对于函数
确定,对于函数![]() 给出下列命题:
给出下列命题:
①对任意![]()
![]() ,都有
,都有![]() 恒成立:
恒成立:
②![]()
![]() ,使得
,使得![]() 且
且![]() 同时成立;
同时成立;
③对于任意![]()
![]() 恒成立;
恒成立;
④对任意,![]()
![]()
![]() ,
,
都有![]() 恒成立.其中正确的命题共有( )
恒成立.其中正确的命题共有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)如果等比数列![]() 共有2016项,其首项与公比均为2,在数列
共有2016项,其首项与公比均为2,在数列![]() 的每相邻两项
的每相邻两项![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() 后,得到一个新的数列
后,得到一个新的数列![]() .求数列
.求数列![]() 中所有项的和;
中所有项的和;
(3)是否存在实数![]() ,使得存在
,使得存在![]() ,使不等式
,使不等式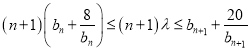 成立,若存在,求实数
成立,若存在,求实数![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com