
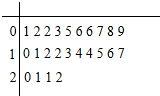 为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.
为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.分析 (1)由茎叶图得24个样本中,康复时间在7周之内(含7周)的样本个数为8个,由此能求出这24个样本中达到快效时间的频率.
(2)由已知得X的可能取值为0,1,2,3,X~B(3,$\frac{1}{3}$),由此能求出X的分布列和EX.
解答 解:(1)由茎叶图得24个样本中,康复时间在7周之内(含7周)的样本个数为8个,
∴这24个样本中达到快效时间的频率p=$\frac{8}{24}=\frac{1}{3}$.
(2)由已知得X的可能取值为0,1,2,3,X~B(3,$\frac{1}{3}$),
P(X=0)=$(\frac{2}{3})^{3}$=$\frac{8}{27}$,
P(X=1)=${C}_{3}^{1}(\frac{1}{3})(\frac{2}{3})^{2}$=$\frac{4}{9}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{3})^{2}(\frac{2}{3})$=$\frac{2}{9}$,
P(X=3)=${C}_{3}^{3}(\frac{1}{3})^{3}$=$\frac{1}{27}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{27}$ | $\frac{4}{9}$ | $\frac{2}{9}$ | $\frac{1}{27}$ |
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | 500 | C. | 600 | D. | 450 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | |
| B. | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
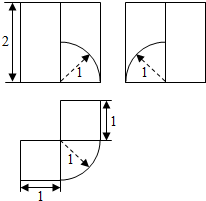
| A. | 6+$\frac{π}{8}$ | B. | 6+$\frac{π}{6}$ | C. | 4+$\frac{π}{8}$ | D. | 4+$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | -1<a<1 | C. | -1<a<1且a≠0 | D. | a>1或a<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com