练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，将绘有函数f（x）=2sin（ωx+φ）（ω＞0， ＜φ＜π）部分图象的纸片沿x轴折成直二面角，若AB之间的空间距离为 ，则f（﹣1）=（ ）

    A.﹣2
    B.2
    C.-
    D.

    【答案】B
    【解析】解：由函数的图象可得2sinφ=1，可得sinφ= ，再根据 ＜φ＜π，可得φ= ．
    再根据A、B两点之间的距离为 = ，求得T=6，
    再根据T= =6，求得ω= ．
    ∴f（x）=2sin（ x+ ），f（﹣1）=2sin（﹣ + ）=2，
    故选：B．
    根据图象过点（0，1），结合φ的范围求得φ的值，再根据A、B两点之间的距离为 = ，求得T的值，可得ω的值，从而求得函数的解析式，从而求得f（﹣1）的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，且∠DAB=90°，∠ABC=45°，CB= ，AB=2，PA=1．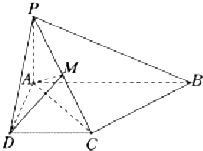

    （1）求证：BC⊥平面PAC；
    （2）若M是PC的中点，求二面角M﹣AD﹣C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设全集为R，函数 的定义域为M，则RM为（ ）
    A.（2，+∞）
    B.（﹣∞，2）
    C.（﹣∞，2]
    D.[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，

    续保人本年度的保费与其上年度出险次数的关联如下：

    上年度出险次数

    0

    1

    2

    3

    4

    保费

    随机调查了该险种的400名续保人在一年内的出险情况，得到如下统计表：

    出险次数

    0

    1

    2

    3

    4

    频数

    120

    100

    60

    60

    40

    20

    （Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求的估计值；

    （Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的190％”.

    求的估计值；

    （III）求续保人本年度的平均保费估计值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2x2﹣4x+a，g（x）=logax（a＞0且a≠1）．
    （1）若函数f（x）在[﹣1，2m]上不具有单调性，求实数m的取值范围；
    （2）若f（1）=g（1）．
    （ⅰ）求实数a的值；
    （ⅱ）设 ，t2=g（x）， ，当x∈（0，1）时，试比较t1 ， t2 ， t3的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列各组函数中，表示同一个函数的是（ ）
    A.y= 与y=x+1
    B.y=lgx与y= lgx2
    C.y= ﹣1与y=x﹣1
    D.y=x与y=logaax（a＞0且a≠1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，比较与1的大小；

    （2）当时，如果函数仅有一个零点，求实数的取值范围；

    （3）求证：对于一切正整数，都有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 的定义域是一切实数，则m的取值范围是（ ）
    A.0＜m≤4
    B.0≤m≤1
    C.m≥4
    D.0≤m≤4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司的两个部门招聘工作人员，应聘者从 T1、T2两组试题中选择一组参加测试，成绩合格者可签约．甲、乙、丙、丁四人参加应聘考试，其中甲、乙两人选择使用试题 T1 ， 且表示只要成绩合格就签约；丙、丁两人选择使用试题 T2 ， 并约定：两人成绩都合格就一同签约，否则两人都不签约．已知甲、乙考试合格的概率都是 ，丙、丁考试合格的概率都是 ，且考试是否合格互不影响．
    （1）求丙、丁未签约的概率；
    （2）记签约人数为 X，求 X的分布列和数学期望EX．

    查看答案和解析>>

    同步练习册答案