
【题目】如图,有一段河流,河的一侧是以O为圆心,半径为![]() 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧![]() 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为![]() ,
,![]() 和
和![]() .
.

(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某家具厂有方木料 ![]() ,五合板
,五合板 ![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料 ![]() ,五合板
,五合板 ![]() ,生产每个书橱需要方木料
,生产每个书橱需要方木料 ![]() ,五合板
,五合板 ![]() ,出售一张书桌可获利润
,出售一张书桌可获利润 ![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润 ![]() 元.
元.
(1)如果只安排生产书桌,可获利润多少?
(2)如果只安排生产书橱,可获利润多少?
(3)怎祥安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在区间![]() 上的函数
上的函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() 成立,那么称函数
成立,那么称函数![]() 在区间
在区间![]() 上可被
上可被![]() 替代,
替代,![]() 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:
①![]() 在区间
在区间![]() 上可被
上可被![]() 替代;
替代;
②![]() 可被
可被![]() 替代的一个“替代区间”为
替代的一个“替代区间”为![]() ;
;
③![]() 在区间
在区间![]() 可被
可被![]() 替代,则
替代,则![]() ;
;
④![]() (
(![]() ),
),![]() (
(![]() ),则存在实数
),则存在实数![]() (
(![]() ),使得
),使得![]() 在区间
在区间![]() 上被
上被![]() 替代; 其中真命题有 .
替代; 其中真命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() :
: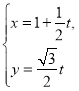 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() 满足
满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 为定义在
为定义在![]() 上的“局部奇函数”;
上的“局部奇函数”;
![]() 方程
方程![]() 有两个不等实根;
有两个不等实根;
若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求
”为真命题,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,满足
的前n项和,满足![]() ,正项等比数列
,正项等比数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() .
.
(Ⅰ) 求数列{an}和{bn}的通项公式; (Ⅱ) 记![]()
![]() ,求数列{cn}的前n项和
,求数列{cn}的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 分别为左右焦点.
分别为左右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,椭圆上有两个点
,椭圆上有两个点![]() 满足
满足![]() 三点共线,
三点共线,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com