
【题目】面积为2的![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线EF上,则
在直线EF上,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据△ABC的面积为2,可得△PBC的面积=1,从而可得PB×PC![]() ,故
,故![]() PB×PCcos∠BPC
PB×PCcos∠BPC![]() ,由余弦定理,有:BC2=BP2+CP2﹣2BP×CPcos∠BPC,进而可得BC2≥2BP×CP﹣2BP×CPcos∠BPC.
,由余弦定理,有:BC2=BP2+CP2﹣2BP×CPcos∠BPC,进而可得BC2≥2BP×CP﹣2BP×CPcos∠BPC.
从而![]() ,利用导数,可得
,利用导数,可得![]() 最大值为
最大值为![]() ,从而可得
,从而可得![]() 的最小值.
的最小值.
解:∵E、F是AB、AC的中点,∴EF到BC的距离=点A到BC的距离的一半,
∴△ABC的面积=2△PBC的面积,而△ABC的面积=2,∴△PBC的面积=1,
又△PBC的面积![]() PB×PCsin∠BPC,∴PB×PC
PB×PCsin∠BPC,∴PB×PC![]() .
.
∴![]() PB×PCcos∠BPC
PB×PCcos∠BPC![]() .
.
由余弦定理,有:BC2=BP2+CP2﹣2BP×CPcos∠BPC.
显然,BP、CP都是正数,∴BP2+CP2≥2BP×CP,∴BC2≥2BP×CP﹣2BP×CPcos∠BPC.
∴![]() PB×PCcos∠BPC+2BP×CP﹣2BP×CPcos∠BPC
PB×PCcos∠BPC+2BP×CP﹣2BP×CPcos∠BPC![]()
令y![]() ,则y′
,则y′![]()
令y′=0,则cos∠BPC![]() ,此时函数在(0,
,此时函数在(0,![]() )上单调增,在(
)上单调增,在(![]() ,1)上单调减
,1)上单调减
∴cos∠BPC![]() 时,
时,![]() 取得最大值为
取得最大值为![]()
∴![]() 的最小值是
的最小值是![]()
故选:D


科目:高中数学 来源: 题型:
【题目】在新冠病毒肆虐全球的大灾难面前,中国全民抗疫,众志成城,取得了阶段性胜利,为世界彰显了榜样力量.为庆祝战疫成功并且尽快恢复经济,某网络平台的商家进行有奖促销活动,顾客购物消费每满600元,可选择直接返回60元现金或参加一次答题返现,答题返现规则如下:电脑从题库中随机选出一题目让顾客限时作答,假设顾客答对的概率都是0.4,若答对题目就可获得120元返现奖励,若答错,则没有返现.假设顾客答题的结果相互独立.
(1)若某顾客购物消费1800元,作为网络平台的商家,通过返现的期望进行判断,是希望顾客直接选择返回180元现金,还是选择参加3次答题返现?
(2)若某顾客购物消费7200元并且都选择参加答题返现,请计算该顾客答对多少次概率最大,最有可能返回多少现金?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线C1:ρ=2cosθ和曲线C2:ρcosθ=3,以极点O为坐标原点,极轴为x轴非负半轴建立平面直角坐标系.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)若点P是曲线C1上一动点,过点P作线段OP的垂线交曲线C2于点Q,求线段PQ长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为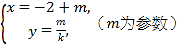 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com