B
分析:已知等值域变换的定义,分别求出f(x)和g(x)的值域和定义域,对①②③④进行一一验证,从而求解;
解答:①函数f(x)=2x+b,x∈R的值域为R,
∵x=t
2-2t+3=(t-1)
2+2≥2,
∴y=f(g(t))=2[(t-1)
2+2]+b≥4+b,值域不一样,
所以,x=g(t)不是f(x)的一个等值域变换,故①错误;
②可得f(x)=|x|≥0,值域大于等于0,
∵
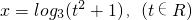
,
∴y=f(g(t))=|

|=

>0,值域大于0,
所以,x=g(t)不是f(x)的一个等值域变换,故②错误;
③若f(x)=x
2-x+1=(x-

)
2+

≥

,
∵x=g(t)=2
t,
∴y=f(g(t))=(2
t-

)
2+

≥

,
∴x=g(t)是f(x)的一个等值域变换,故③正确;
④f(x)=log
2x(x>0),值域为R,
∵x=g(t)=5
t+5
-t+m是y=f(x)的一个等值域变换,
∴函数f(g(t))的定义域为R,值域也为R,
∴f(g(t))=log
2(5
t+5
-t+m)的值域为R,可得5
t+5
-t+m≤0即可,所以m≤-(5
t+5
-t)≤-2,在R上恒成立,
∴m≤-2,故④正确,
故选B;
点评:考查新定义,解题的关键的是能够读懂新定义,利用了整体代换的思想,是一道综合题;

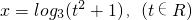 ,则x=g(t)是f(x)的一个等值域变换;
,则x=g(t)是f(x)的一个等值域变换;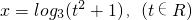 ,
, |=
|= >0,值域大于0,
>0,值域大于0, )2+
)2+ ≥
≥ ,
, )2+
)2+ ≥
≥ ,
,

 阅读快车系列答案
阅读快车系列答案