练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，满足tanA•tanB＞1，则这个三角形是


    1. A.
      正三角形
    2. B.
      等腰三角形
    3. C.
      锐角三角形
    4. D.
      钝角三角形
    C
    分析：由条件可得A、B都是锐角，tanA＞0，tanB＞0，再由 tan（A+B）=＜0，可得A+B为钝角，C为锐角，与偶此得出结论．
    解答：∵在△ABC中，满足tanA•tanB＞1，∴A、B都是锐角，tanA＞0，tanB＞0．
    再由 tan（A+B）=＜0，可得A+B为钝角，故由三角形内角和公式可得C为锐角．
    综上可得这个三角形是锐角三角形．
    故选C．
    点评：本题主要考查两角和的正切公式、三角形内角和公式的应用，判断三角形的形状，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在△ABC中，AD⊥BC，
    AD
    =
    1
    5
    AB
    +
    4
    5
    AC
    ．
    （1）求
    |
    CD
    |
    |
    DB
    |
    的值；
    （2）设cosC=
    		5
    5
    ，且实数t满足|
    CB
    -t
    CA
    |≥|
    AB
    +
    AC
    |    ，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题：
    （1）若函数f（x）=lg（x+
    		x2+a
    ），为奇函数，则a=1；
    （2）函数f（x）=|sinx|的周期T=π；
    （3）已知
    a
    =(sinθ，
    		1+cosθ
    )，
    b
    =(1，
    		1-cosθ
    )    ，其中θ∈（π，
    3π
    2
    ），则
    a
    ⊥
    b

    （4）在△ABC中，
    BA
    =a，
    AC
    =b，若a•b＜0，则△ABC是钝角三角形
    （ 5）O是△ABC所在平面上一定点，动点P满足：
    OP
    =
    OA
    +λ(
    AB
    sinC
    +
    AC
    sinB
    )    ，λ∈（0，+∞），则直线AP一定通过△ABC的内心．
    以上命题为真命题的是
    （1）（2）（3）（5）
    （1）（2）（3）（5）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，AC=10，过顶点C作AB的垂线，垂足为D，AD=5，且满足
    AD
    =
    5
    11
    DB
    ．
    （1）求|
    AB
    -
    AC
    |    ；
    （2）存在实数t≥1，使得向量x=
    AB
    +t
    AC
     ， y=t
    AB
    +
    AC
    ，令k=x•y，求k的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (本小题12分)

    在△ABC中, 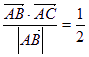 ,  , 又点E在BC边上, 且满足 ,以A、B为焦点的双曲线经过C、E两点.

    (1)求此双曲线的方程.

    (2)设M、N为双曲线在第一象限内不同的两点，若x轴上一点T到点M、N的距离相等，求点T横坐标的取值范围

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省淄博市临淄中学高三（上）第二次月考数学试卷（文科）（解析版） 题型：填空题

    下列命题：
    （1）若函数f（x）=lg（x+），为奇函数，则a=1；
    （2）函数f（x）=|sinx|的周期T=π；
    （3）已知，其中θ∈（π，），则
    （4）在△ABC中，=a，=b，若a•b＜0，则△ABC是钝角三角形
    （ 5）O是△ABC所在平面上一定点，动点P满足：，λ∈（0，+∞），则直线AP一定通过△ABC的内心．
    以上命题为真命题的是    ．

    查看答案和解析>>

    同步练习册答案