
如图所示,在菱形ABCD中,∠DAB = 60°,PA⊥底面ABCD,PA = AB = 2,E、F分别是AB与PD的中点.
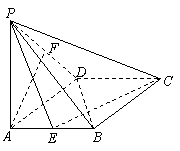 (1) 求证:PC⊥BD;
(1) 求证:PC⊥BD;
(2) 求证:AF∥平面PEC;
(3) 求二面角P - EC - D的大小.
 解:(1) 证明:(1)连接AC,则AC⊥BD。
解:(1) 证明:(1)连接AC,则AC⊥BD。
∵PA⊥平面ABCD,AC是斜线PC在平面ABCD
上的射影,∴由三垂线定律得PC⊥BD
(2) 取PC中点K,连接FK 、EK,
则四边形AEKF是平行四边形,
∴ AF∥EK,又EK  平面PEC,AF
平面PEC,AF 平面PEC,
平面PEC,
∴ AF∥平面PEC
(3) 延长DA、CE交于M,过A作AH⊥CM与H,
连结PH,由于PA⊥平面ABCD,可得PH⊥CM。
∴ ∠PHA为所求二面角P-EC-D的平面角。
∵ E为AB的中点,AE∥CD,∴AM=AD=2 ,
在△AME中,∠MAE=120°,
由余弦定理得EM2=AM2+AEAM·AEcos120°=7,
EM=, 又S△AME=AH·EM=AM·AE·sim120°,
∴AH = ,∴ tan∠PHA= = .
∴ 二面角P-EC-D的大小为arctan.


科目:高中数学 来源: 题型:
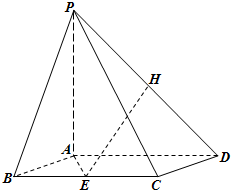 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且AB=2,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且AB=2,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:学习高手必修二数学苏教版 苏教版 题型:044
如图所示,在菱形ABCD中,∠ABC=60°,PA⊥平面AC,AB=PA=a,PE=EA,求C到平面BDE的距离.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃甘谷一中宏志班选拔考试数学试卷(解析版) 题型:选择题
如图所示,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
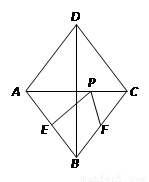
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com