
项目 类别 | 年固定 成本 | 每件产品 成本 | 每件产品 销售价 | 每年最多可 生产的件数 |
| A产品 | 20 | m | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
分析 (1)利用“利润=收入-成本”分别代入计算即得结论;
(2)通过(1)分别计算出两种产品的年利润最大值,进而作差比较即得结论.
解答 解:(1)由年销售量为x件,按利润的计算公式,有生产A、B两产品的年利润y1,y2分别为:
y1=10x-(20+cx)=(10-c)x-20(0≤x≤200且x∈N),
y2=18x-(40+8x)-0.05x2=-0.05(x-100)2+460(0≤x≤120且x∈N),
(2)∵6≤c≤9,
∴10-c>0,
∴y1=(10-c)x-20为增函数,
又∵0≤x≤200,x∈N,
∴当x=200时,生产A产品有最大利润为(10-c)×200-20=1980-200c(万美元),
又∵y2=-0.05(x-100)2+460(0≤x≤120且x∈N),
∴当x=100时,生产B产品有最大利润为460,
因为(y1)max-(y2)max=(1980-200c)-460=1520-200c=$\left\{\begin{array}{l}{>0,}&{6≤c<7.6}\\{=0,}&{c=7.6}\\{<0,}&{7.6<c≤9}\end{array}\right.$,
所以,当6≤c<7.6时,可投资生产A产品200件;
当c=7.6时,生产A产品与生产B产品均可;
当7.6<c≤9时,可投资生产B产品100件.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
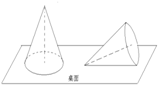 用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn单调递减 | B. | Sn单调递增 | C. | Sn有最大值 | D. | Sn有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com