
利用某些已经证明的不等式,从________出发,运用不等式的________推出所要证的不等式,这种证明不等式的方法叫做综合法.其思维特点是________,即从________逐步向________靠拢.
科目:高中数学 来源: 题型:
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 13 |
| 24 |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
查看答案和解析>>
科目:高中数学 来源:2010年大连市高二下学期六月月考理科数学卷 题型:选择题
利用数学归纳法证明“ ”的过程中,
”的过程中,
由“n=k”变到“n=k+1”时,不等式左边的变化是 ( )
(A)增加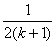 (B)增加
(B)增加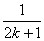 和
和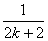
(C)增加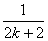 ,并减少
,并减少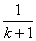 (D)增加
(D)增加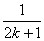 和
和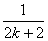 ,并减少
,并减少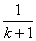
查看答案和解析>>
科目:高中数学 来源:2010年云南省昆明八中高考数学二模试卷(理科)(解析版) 题型:选择题
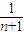 +
+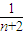 +…+
+…+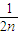 >
> (n>1且n∈N)时,在证明n=k+1这一步时,需要证明的不等式是( )
(n>1且n∈N)时,在证明n=k+1这一步时,需要证明的不等式是( )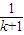 +
+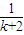 +…+
+…+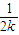 >
>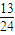
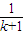 +
+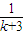 +…+
+…+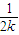 +
+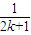 >
>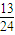
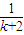 +
+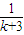 +…+
+…+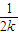 +
+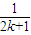 >
>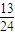
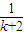 +
+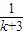 +…+
+…+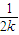 +
+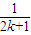 +
+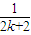 >
>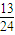
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第五次质量检测文科数学试卷(解析版) 题型:解答题
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明:
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f(x)在[1,2]上是减函数,的导函数恒小于等于零,然后分离参数求解得到a的取值范围。第二问中,
假设存在实数a,使 有最小值3,利用
有最小值3,利用 ,对a分类讨论,进行求解得到a的值。
,对a分类讨论,进行求解得到a的值。
第三问中,
因为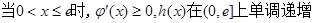 ,这样利用单调性证明得到不等式成立。
,这样利用单调性证明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)见解析
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com