
【题目】已知![]()
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)f(x)=2x-2-x;定义域为![]() (2)(-∞,-1]
(2)(-∞,-1]
【解析】
(1)利用换元法,求得函数的解析式,并求得定义域.
(2)利用换元法,将原不等式分离常数得到![]() 在
在![]() 恒成立,利用二次函数对称轴,求得
恒成立,利用二次函数对称轴,求得![]() 在
在![]() 上的最小值,进而求得
上的最小值,进而求得![]() 的取值范围.
的取值范围.
(1)设log2x=t,t∈R
可得x=2t
∴f(t)=![]() ,
,
即f(x)=2x-2-x,定义域为![]() .
.
(2)由8x-8-x-4x+1-41-x+8≥kf(x)对x∈[1,+∞)恒成立,
即8x-8-x-4x+1-41-x+8≥k(2x-2-x)对x∈[1,+∞)恒成立,
可得(2x)3-(2-x)3-4[(2x)2+(2-x)2]+8≥k(2x-2-x)
则(2x-2-x)[(2x)2+(2-x)2+1]-4[(2x)2+(2-x)2]+8≥k(2x-2-x)
∴(2x-2-x)[(2x-2-x)2+3]-4[(2x-2-x)2+2]+8≥k(2x-2-x)
∴(2x-2-x)[(2x-2-x)2+3]-4(2x-2-x)2≥k(2x-2-x)
设2x-2-x=t,
可得t(t2+3)-4t2≥kt,(t∈R)
∵x∈[1,+∞)恒成立,
∴t≥![]()
则t2+3-4t≥k在t∈[![]() ,+∞)恒成立,
,+∞)恒成立,
当t=2时,(t2+3-4t)min=-1
∴k≤-1;
故得k的取值范围是(-∞,-1];


科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() ,
,![]() 两组.
两组.![]() 年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() ,
,![]() ,
,![]() ,
,![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
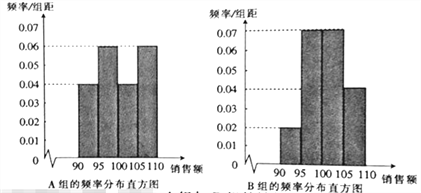
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() ,
,![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市关系要好的![]() 四个家庭各有两个小孩共8人,准备使用滴滴打车软件,分乘甲、乙两辆汽车出去游玩,每车限坐4人,(乘同一辆车的4名小孩不考虑位置差异).
四个家庭各有两个小孩共8人,准备使用滴滴打车软件,分乘甲、乙两辆汽车出去游玩,每车限坐4人,(乘同一辆车的4名小孩不考虑位置差异).
(1)共有多少种不同的乘坐方式?
(2)若![]() 户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有多少种?
户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
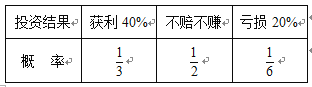
【题目】某理财公司有两种理财产品![]() 和
和![]() .这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
产品![]() (其中
(其中![]() )
)
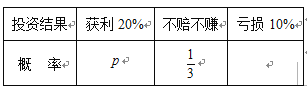
(Ⅰ)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于
进行投资,如果一年后他们中至少有一人获利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解一家企业生产的某类产品的使用寿命(单位:小时),现从中随机抽取一定数量的产品进行测试,绘制频率分布直方图如图所示.

(1)假设同一组中的每个数据可用该组区间的中点值代替,估算这批产品的平均使用寿命;
(2)已知该企业生产的这类产品有甲、乙两个系列,产品使用寿命不低于60小时为合格,合格产品中不低于90小时为优异,其余为一般.现从合格产品中,用分层抽样的方法抽取70件,其中甲系列有35件(1件优异).请完成下面的列联表,并根据列联表判断能否有![]() 的把握认为产品优异与系列有关?
的把握认为产品优异与系列有关?
甲系列 | 乙系列 | 合计 | |
优异 | |||
一般 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公交车的数量太多容易造成资源浪费,太少又难以满足乘客的需求,为了合理布置车辆,公交公司在2路车的乘客中随机调查了50名乘客,经整理,他们候车时间(单位:![]() )的茎叶图如下:
)的茎叶图如下:

(Ⅰ)将候车时间分为![]() 八组,作出相应的频率分布直方图;
八组,作出相应的频率分布直方图;

(Ⅱ)若公交公司将2路车发车时间调整为每隔15![]() 发一趟车,那么上述样本点将发生变化(例如候车时间为9
发一趟车,那么上述样本点将发生变化(例如候车时间为9![]() 的不变,候车时间为17
的不变,候车时间为17![]() 的变为2
的变为2![]() ),现从2路车的乘客中任取5人,设其中候车时间不超过10
),现从2路车的乘客中任取5人,设其中候车时间不超过10![]() 的乘客人数为
的乘客人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com