
 解:这是一个几何概型问题.
解:这是一个几何概型问题.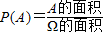
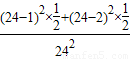
 .
.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一昼夜内到达该码头的时刻是等可能的,如果甲船停泊时间为1h,乙船停泊时间为2h,求它们中的任意一艘都不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源:2010-2011年甘肃省高一下学期期中考试数学 题型:解答题
(本小题12分) [来源:学&科&网Z&X&X&K]
甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一昼夜内到达码头的时刻是等可能的,如果甲船停泊时间为1h,乙船停泊时间为2h,求它们中的任意一艘都不需要等待码头空出的概率. (精确到0.001)
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com