
【题目】在![]() 中,已知
中,已知![]() ,分别根据下列条件求
,分别根据下列条件求![]() (精确到0.01°).
(精确到0.01°).
(1)①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;
;
(2)根据上述计算结果,讨论使![]() 有一个解、两个解、无解时,
有一个解、两个解、无解时,![]() 的取值情况.
的取值情况.
科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
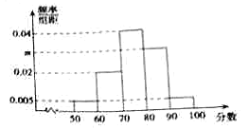
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
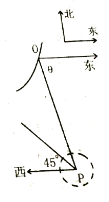
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300千米的海面
方向300千米的海面![]() 处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与圆
与圆![]() 的两个交点分别为
的两个交点分别为![]() ,
, ![]() ,求证:
,求证: 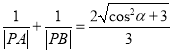 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校学生喜欢吃零食是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人,抽到不喜欢吃零食的学生的概率为![]() .
.
喜欢吃零食 | 不喜欢吃零食辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
(Ⅰ)请将上面的列表补充完整;
(Ⅱ)是否有99.9%以上的把握认为喜欢吃零食与性别有关?说明理由.
下面的临界值表供参考:![]() ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.

(Ⅰ)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(Ⅱ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为1000元,空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天,求这两天的净化空气总费用为3000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)试探究当![]() 时,方程
时,方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在航天员进行的一项太空实验中,要先后实施6个程序,其中程序![]() 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序![]() 实施时必须相邻,请问实验顺序的编排方法共有 ( )
实施时必须相邻,请问实验顺序的编排方法共有 ( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com