
必做题
已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() (与原点不重合)在抛物线上.
(与原点不重合)在抛物线上.
(1)作一条斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,连接
两点,连接![]() 分别交
分别交![]() 轴于
轴于![]() 两点,(直线
两点,(直线![]() 与
与![]() 轴不垂直),求证
轴不垂直),求证![]() ;
;
(2)设![]() 为抛物线上两点,过
为抛物线上两点,过![]() 作抛物线的两条切线相交于点
作抛物线的两条切线相交于点![]() ,(
,(![]() 与
与![]() 不重合,与
不重合,与![]() 的连线也不垂直于
的连线也不垂直于![]() 轴),求证:
轴),求证:![]() .
.
(1)由题设知:![]() ,直线
,直线![]() ,
,![]() 的斜率存在,分别设为
的斜率存在,分别设为![]()
直线![]() 的方程为:
的方程为:![]()
由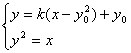
得![]() ………………………………………………1分
………………………………………………1分
直线![]() 的方程为:
的方程为:![]()
由 得
得![]() …………………………2分
…………………………2分
带入![]() 化简得:
化简得:![]() , ……………………………………4分
, ……………………………………4分
![]()
![]()
![]()
![]() ………………………………………………5分
………………………………………………5分
(2)设![]() ,
,![]()
抛物线在![]() 点处的切线斜率为
点处的切线斜率为![]() (把抛物线方程转化为函数解析式,利用导数求切线斜率,或者设出直线方程与抛物线方程联立,利用
(把抛物线方程转化为函数解析式,利用导数求切线斜率,或者设出直线方程与抛物线方程联立,利用![]() ,求出斜率为
,求出斜率为![]() )
)
直线![]() 的方程为:
的方程为:![]() 即
即![]()
同理可得直线![]() 的方程为:
的方程为:![]() …………………7分
…………………7分
由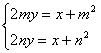 得
得![]() ……………………………………8分
……………………………………8分
直线![]() 的方程为:
的方程为:![]()
点![]() 到直线
到直线![]() 的距离
的距离
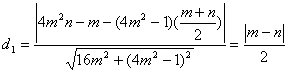
点![]() 到直线
到直线![]() 的距离
的距离![]() ……………………………9分
……………………………9分
![]() ………………………………………………10分
………………………………………………10分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
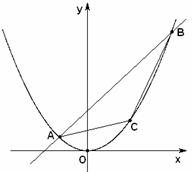
【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
已知直线![]() 被抛物线
被抛物线![]() 截得的弦长
截得的弦长![]() 为20,
为20,![]() 为坐标原点.
为坐标原点.
(1)求实数![]() 的值;
的值;
(2)问点![]() 位于抛物线弧
位于抛物线弧![]() 上何处时,△
上何处时,△![]() 面积最大?
面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【必做题】已知抛物线![]() ,直线
,直线![]() 与抛物线C交于点A,B,与
与抛物线C交于点A,B,与![]() 轴交于点M.
轴交于点M.
(1)若抛物线焦点坐标为![]() ,求直线
,求直线![]() 与抛物线C围成的面积;
与抛物线C围成的面积;
(2)直线![]() 与抛物线C交于异于原点的点P,MP交抛物线C于另一点Q,求证:当
与抛物线C交于异于原点的点P,MP交抛物线C于另一点Q,求证:当![]() 变化时,点Q在一条定直线上.
变化时,点Q在一条定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com