
【题目】已知正三棱柱![]() 中,所有棱长都是3,点D,E分别是线段
中,所有棱长都是3,点D,E分别是线段![]() 和
和![]() 上的点,
上的点,![]() .
.
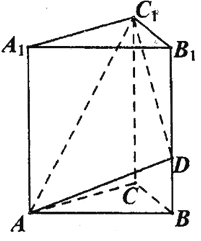
(1)试确定点E的位置,使得![]() 平面
平面![]() ,并证明;
,并证明;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值的大小.
的余弦值的大小.
【答案】(1)E为![]() 三等分点,且
三等分点,且![]() ,证明见解析;(2)
,证明见解析;(2)![]()
【解析】
(1)取E为AC的三等分点,且AC=3AE,过E作EK∥CC1,且![]() ,得到四边形BEKD为平行四边形,有BE∥KD,由线面平行的判定可得BE∥平面ADC1;
,得到四边形BEKD为平行四边形,有BE∥KD,由线面平行的判定可得BE∥平面ADC1;
(2)设AC中点为M,设A1C1的中点为P,分别以MA,MB,MP所在直线为x,y,z轴建立空间直角坐标系.由直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,可得E点坐标为
,可得E点坐标为![]() ,然后分别求出平面ABE与平面BEC1的一个法向量,由两法向量所成角的余弦值可得二面角A-BE-C1的余弦值.
,然后分别求出平面ABE与平面BEC1的一个法向量,由两法向量所成角的余弦值可得二面角A-BE-C1的余弦值.
(1)取E为![]() 三等分点,且
三等分点,且![]() ,过E作
,过E作![]() ,
,
则![]() ,所以
,所以![]() 为平行四边形,
为平行四边形,
所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,证毕;
,证毕;
(2)设![]() 中点为M,设
中点为M,设![]() 中点为P,
中点为P,
分别以![]() ,
,![]() ,
,![]() 为x,y,z建立空间直角坐标系,
为x,y,z建立空间直角坐标系,
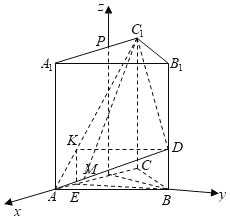
则A(![]() ,0,0),C(
,0,0),C(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),
,0),![]() (
(![]() ,0,3),
,0,3),
 ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由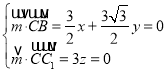 ,取
,取![]() ,
,
可得![]() ,
,
设E点坐标为![]() ,
,
![]() ,
,
由直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,

解得![]() ,
,
可得E点坐标为![]() ,
,
即![]() ,
,
易求平面![]() 法向量
法向量![]() ,
,
设平面![]() 法向量
法向量![]() ,
,
 ,
,![]() ,
,
由 ,取
,取![]() ,
,
可得 ,
,
 ,
,
又因为二面角![]() 为钝角,
为钝角,
所以所求余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
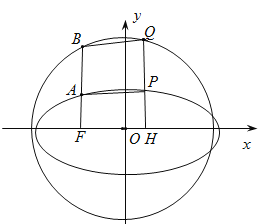
(2)已知圆![]() ,连接
,连接![]() 并延长交圆
并延长交圆![]() 于点
于点![]() 为椭圆长轴上一点(异于左、右焦点),过点
为椭圆长轴上一点(异于左、右焦点),过点![]() 作椭圆长轴的垂线分别交椭圆
作椭圆长轴的垂线分别交椭圆![]() 和圆
和圆![]() 于点
于点![]() (
(![]() 均在
均在![]() 轴上方).连接
轴上方).连接![]() ,记
,记![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() .
.
①求![]() 的值;
的值;
②求证:直线![]() 的交点在定直线上.
的交点在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从![]() 年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取
年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取![]() 个,并按
个,并按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
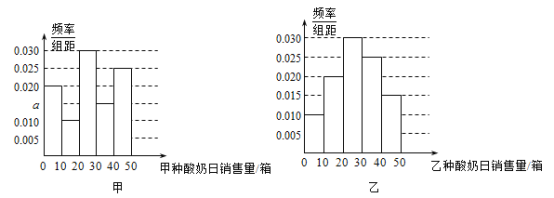
(1)写出频率分布直方图甲中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 、
、![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于![]() 箱且另一个不高于
箱且另一个不高于![]() 箱的概率;
箱的概率;
(3)设![]() 表示在未来
表示在未来![]() 天内甲种酸奶的日销售量不高于
天内甲种酸奶的日销售量不高于![]() 箱的天数,以日留住量落入各组的频率为概率,求
箱的天数,以日留住量落入各组的频率为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为
的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 〔
〔![]() >b>0〕与抛物线
>b>0〕与抛物线![]() 有共同的焦点F,且两曲线在第一象限的交点为M,满足
有共同的焦点F,且两曲线在第一象限的交点为M,满足![]() .
.
(1)求椭圆的方程;
(2)过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,设
两点,设![]() ,假设
,假设![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com