
科目:高中数学 来源:不详 题型:填空题
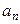 }满足
}满足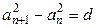 (其中d是常数,
(其中d是常数,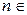 N﹡),则称数列{
N﹡),则称数列{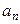 }是“等方差数列”. 已知数列{
}是“等方差数列”. 已知数列{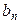 }是公差为m的差数列,则m=0是“数列{
}是公差为m的差数列,则m=0是“数列{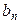 }是等方差数列”的 条件。(填充分不必要、必要不充分、充要条件、既不充分也不必要条件中的一个)
}是等方差数列”的 条件。(填充分不必要、必要不充分、充要条件、既不充分也不必要条件中的一个)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
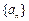 的前
的前 项和为
项和为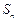 ,其中
,其中 ,
,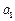 为常数,且
为常数,且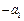 、
、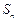 、
、 成等差数列.
成等差数列.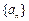 的通项公式;
的通项公式;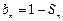 ,问:是否存在
,问:是否存在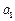 ,使数列
,使数列 为等比数列?若存在,求出
为等比数列?若存在,求出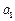 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.2006 | B.4008 | C.4012 | D.2008 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
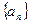 中,
中,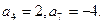 现从
现从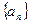 的前10项中随机取数,每次取出一个数,取后放回,连续抽取3次,假定每次取数互不影响,那么在这三次取数中,取出的数恰好为两个正数和一个负数的概率为 (用数字作答).
的前10项中随机取数,每次取出一个数,取后放回,连续抽取3次,假定每次取数互不影响,那么在这三次取数中,取出的数恰好为两个正数和一个负数的概率为 (用数字作答).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
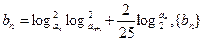 的前n项和为Tn,求
的前n项和为Tn,求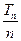 的最小值.
的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com