
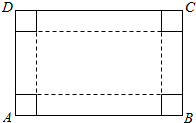
 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).分析 (1)求出纸箱的侧面积S,利用基本不等式,求最大值;
(2)求出纸箱的容积V,利用导数,求最大值.
解答 解:(1)S=2x(50-2x+80-2x)=2x(130-4x)≤$\frac{1}{2}$•$(\frac{4x+130-4x}{2})^{2}$=$\frac{4225}{2}$,
当且仅当4x=130-4x,即x=$\frac{65}{4}$cm,纸箱的侧面积S(cm2)最大;
(2)V=x(50-2x)(80-2x)(0<x<12.5),
V′=(50-2x)(80-2x)-2x(80-2x)-2x(50-2x)=4(3x-100)(x-10),
∴0<x<10,V′>0,10<x<12.5,V′<0,
∴x=10cm时,V最大.
点评 (1)解有关函数最大值、最小值的实际问题,需要分析问题中各个变量之间的关系,找出适当的函数关系式,并确定函数的定义区间;所得结果要符合问题的实际意义.(2)根据问题的实际意义来判断函数最值时,如果函数在此区间上只有一个极值点,那么这个极值就是所求最值,不必再与端点值比较.(3)相当多有关最值的实际问题用导数方法解决较简单


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
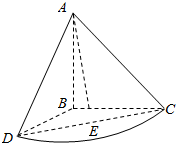 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
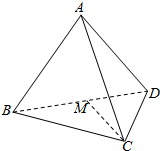 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com