
【题目】如图所示, ![]() 是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为
是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为![]() 平分千米的三角形主题游戏乐园
平分千米的三角形主题游戏乐园![]() ,并在区域
,并在区域![]() 建立水上餐厅.
建立水上餐厅.
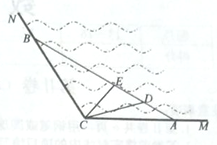
已知![]() ,
, ![]() .
.
(1)设![]() ,
, ![]() ,用
,用![]() 表示
表示![]() ,并求
,并求![]() 的最小值;
的最小值;
(2)设![]() (
(![]() 为锐角),当
为锐角),当![]() 最小时,用
最小时,用![]() 表示区域
表示区域![]() 的面积
的面积![]() ,并求
,并求![]() 的最小值.
的最小值.
【答案】(1) ![]() ;(2)S=
;(2)S=![]() ,8-
,8-![]() .
.
【解析】试题分析:
(1)首先确定函数的解析式为![]() 结合均值不等式的结论可得
结合均值不等式的结论可得![]() 的最小值是
的最小值是![]() ;
;
(2)结合题意和三角函数的性质可得S=![]() ,利用三角函数的性质可知
,利用三角函数的性质可知![]() 的最小值是8-
的最小值是8-![]() .
.
试题解析:
(1)由S△ACB=![]() AC·BC·sin∠ACB=4
AC·BC·sin∠ACB=4![]() 得,BC=
得,BC=![]() ,
,
在△ACB中,由余弦定理可得,AB2=AC2+BC2-2AC·BC·cos∠ACB,
即y2=x 2+![]() +16,
+16,
所以y=![]()
y=![]() ≥
≥![]() =4
=4![]() ,
,
当且仅当x2=![]() ,即x=4时取等号.
,即x=4时取等号.
所以当x=4时,y有最小值4![]() .
.
(2)由(1)可知,AB=4![]() ,AC=BC=4,所以∠BAC=30°,
,AC=BC=4,所以∠BAC=30°,
在△ACD中,由正弦定理,CD=![]() =
=![]() =
=![]() ,
,
在△ACE中,由正弦定理,CE=![]() =
=![]() =
=![]() ,
,
所以,S=![]() CD·CE·sin∠DCE=
CD·CE·sin∠DCE=![]() =
=![]() .
.
因为θ为锐角,
所以当θ=![]() 时,S有最小值8-4
时,S有最小值8-4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(2)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 有且只有一个极值点,求实数
有且只有一个极值点,求实数![]() 的取值范围;
的取值范围;
(2)对于函数![]() ,
,![]() ,
,![]() ,若对于区间
,若对于区间![]() 上的任意一个
上的任意一个![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是函数
是函数![]() ,
,![]() 在区间
在区间![]() 上的一个“分界函数”.已知
上的一个“分界函数”.已知![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得函数
,使得函数![]() 是函数
是函数![]() ,
,![]() 在区间
在区间![]() 上的一个“分界函数”?若存在,求实数
上的一个“分界函数”?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,若
,若![]() 是
是![]() 的三条边长,则下列结论中正确的是( )
的三条边长,则下列结论中正确的是( )
①存在![]() ,使
,使![]() 、
、![]() 、
、![]() 不能构成一个三角形的三条边
不能构成一个三角形的三条边
②对一切![]() ,都有
,都有![]()
③若![]() 为钝角三角形,则存在
为钝角三角形,则存在![]() ,使
,使![]()
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4个男生,3个女生站成一排.(必须写出算式再算出结果才得分)
(Ⅰ)3个女生必须排在一起,有多少种不同的排法?
(Ⅱ)任何两个女生彼此不相邻,有多少种不同的排法?
(Ⅲ)甲乙二人之间恰好有三个人,有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 和
和![]() 分别在
分别在![]() 轴和
轴和![]() 轴上滑动.
轴上滑动.
(1)求线段![]() 的中点的轨迹
的中点的轨迹![]() 的方程;
的方程;
(2)当![]() 时,曲线
时,曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在线段
在线段![]() 上,过
上,过![]() 作
作![]() 轴的垂线交曲线
轴的垂线交曲线![]() 于不同的两点
于不同的两点![]() ,点
,点![]() 在线段
在线段![]() 上,满足
上,满足![]() 与
与![]() 的斜率之积为-2,试求
的斜率之积为-2,试求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高二年段的男生进行体检,现将高二男生的体重![]() 数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组
数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组![]() 的人数为200.根据一般标准,高二男生体重超过
的人数为200.根据一般标准,高二男生体重超过![]() 属于偏胖,低于
属于偏胖,低于![]() 属于偏瘦.观察图形的信息,回答下列问题:
属于偏瘦.观察图形的信息,回答下列问题:
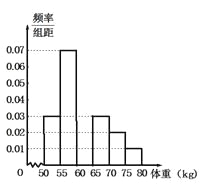
(1)求体重在![]() 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;
(2)用分层抽样的方法从偏胖的学生中抽取![]() 人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com