练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求函数的最小正周期。

    解析：函数的定义域要满足两个条件；

        要有意义且

        ，且

        当原函数式变为时，

        此时定义域为

        显然作了这样的变换之后，定义域扩大了，两式并不等价

        所以周期未必相同，那么怎么求其周期呢？首先作出的图象：

     

        而原函数的图象与的图象大致相同

        只是在上图中去掉所对应的点

        从去掉的几个零值点看，原函数的周期应为

        说明：此题极易由的周期是而得出原函数的周期也是，这是错误的，原因正如上所述。那么是不是说非等价变换周期就不同呢？也不一定，如1993年高考题：函数的最小正周期是（    ）。A.     B.      C.    D. 。此题就可以由的周期为而得原函数的周期也是。但这个解法并不严密，最好是先求定义域，再画出图象，通过空点来观察，从而求得周期。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=sin(2x+
    π
    6
    )+sin(2x-
    π
    6
    )+cos2x+a (a∈R，a    为常数）．
    （1）求函数的最小正周期；
    （2）求函数的单调递增区间；
    （3）若x∈[0，  
    π
    2
    ]    时，f（x）的最小值为-2，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

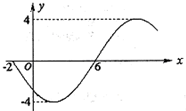    函数y=Asin(ωx+?)(ω＞0，|?|＜
    π2
    ，x∈R)    的部分图象如图所示，
    （1）求函数的最小正周期；（2）求函数解析式；（3）当x∈（-2，8）时，求函数的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=2sinx（sinx+cosx）-1
    （1）求函数的最小正周期
    （2）求函数的递增区间
    （3）画出此函数在区间[-
    π
    2
    ，
    π
    2
    ]    上的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=cos(
    1
    4
    x+
    π
    3
    )    ．
    （1）求函数的最小正周期；
    （2）求函数的对称轴及对称中心；
    （3）求函数的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    		2
    sin（2x-
    π
    4
    ）．
    （1）求f（
    5π
    24
    ）的值；
    （2）求函数的最小正周期；
    （3）用五点法画出一个周期内的图象，列出表格．

    查看答案和解析>>

    同步练习册答案