
【题目】已知点 ![]() ,圆
,圆 ![]() ,过点
,过点 ![]() 的直线l与圆
的直线l与圆 ![]() 交于
交于 ![]() 两点,线段
两点,线段 ![]() 的中点为
的中点为 ![]() (
( ![]() 不同于
不同于 ![]() ),若
),若 ![]() ,则l的方程是 .
,则l的方程是 . 
【答案】![]()
【解析】圆C的标准方程可化为(x﹣2)2+y2=6,
所以圆心为C(2,0),半径为 ![]() ,
,
设M(x,y),则 ![]() =(x﹣2,y),
=(x﹣2,y), ![]() =(1﹣x,1﹣y),
=(1﹣x,1﹣y),
由题设知 ![]()
![]() =0,故(x﹣2)(1﹣x)+y(1﹣y)=0,
=0,故(x﹣2)(1﹣x)+y(1﹣y)=0,
即(x﹣ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]() .
.
由于点P在圆C的内部,
所以M的轨迹方程是(x﹣ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]() .
.
M的轨迹是以点N( ![]() ,
, ![]() )为圆心,
)为圆心, ![]() 为半径的圆.
为半径的圆.
由于|OP|=|OM|,故O在线段PM的中垂线上,
又P在圆N上,从而ON⊥PM.
因为ON的斜率为 ![]() ,所以l的斜率为﹣3,
,所以l的斜率为﹣3,
故l的方程为y﹣1=﹣3(x﹣1),即3x+y﹣4=0.
故答案为:3x+y﹣4=0.
过一定点的直线与圆相交所得的弦的中点轨迹应是一个圆在已知圆内部的一部分,再由 | O P | = | O M |得直线的斜率,求其方程.


科目:高中数学 来源: 题型:
【题目】下列命题:其中正确命题的序号是 .
①设a,b是非零实数,若a<b,则ab2<a2b;
②若a<b<0,则 ![]() >
> ![]() ;
;
③函数y= ![]() 的最小值是2;
的最小值是2;
④若x,y是正数, ![]() +
+ ![]() =1,则x+2y的最小值为8.
=1,则x+2y的最小值为8.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的个数是( )
①若正实数![]() 满足
满足![]() ,则
,则![]() 的最小值是16;
的最小值是16;
②已知![]() ,则函数
,则函数![]() 的最大值为
的最大值为![]() ;
;
③已知![]() ,且
,且![]() ,则
,则![]() 的最小值是36;
的最小值是36;
④若对任意实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]() 。
。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )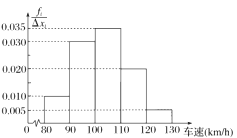
A.30辆
B.1700辆
C.170辆
D.300辆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com