分析:(I)取AC中点F,连接OF、FB,可证四边形BDOF是平行四边形,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(II)以C为原点,分别以CA、CB为x、y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,写出各点的坐标,
设面ODM的法向量
=(x,y,z),则直线CD和平面ODM所成角为θ,从而求解.
(III)取EM中点N,连接ON、CM,因为AC=BC,M为AB中点,可得CM⊥AB,证明ON∥CM即可求解.
解答: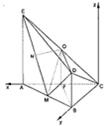
解:(I)证明:取AC中点F,连接OF、FB(1分)
∵F是AC中点,O为CE中点,∴OF∥EA且OF=
EA,又BD∥AE且BD=
AE∴F∥DB,OF=DB
∴四边形BDOF是平行四边形(2分)
∴OD∥FB(3分)
又∵FB?平面MEG,OD?平面MEG
∴OD面ABC.(4分)
(II)∵DB⊥面ABC,
又∵面ABDE⊥面ABC,面ABDE∩面ABC=AB,DB?面ABDE,
∴DB⊥面ABC,
∵BD∥AE,
∴EA⊥面ABC,(5分)
如图,以C为原点,分别以CA、CB为x、y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系
∵AC=BC=4
∴各点坐标为:C(0,0,0),A(4,0,0),B(0,4,0),D(0,4,2)
E(4,0,4)
∴
O(2,0,2),M(2,2,0),=(0,4,2),=(-2,4,0),=(-2,2,2)(6分)
设面ODM的法向量
=(x,y,z),则由
⊥可得
令x=2,
得:
=(2,1,1)(7分)
设直线CD和平面ODM所成角为θ.
则:
sinθ=||=|| (2,1,1)•(0,4,2) |
| |(2,1,1)|•|(0,4,2)| |
|==.
∴直线CD和平面ODM所成角正弦值为
.(8分)
(III)方法一:当N是EM中点时,ON⊥平面ABDE.(9分)
证明:取EM中点N,连接ON、CM,∵AC=BC,M为AB中点,∴CM⊥AB,
又∵面ABDE⊥面ABC,面ABDE∩面ABC=AB,CM?面ABC,
∴CM⊥AB,
∵N是EM中点,O为CE中点,∴ON∥CM,
∴ON⊥平面ABDE.(13分)
方法二当N是EM中点时,ON⊥平面ABDE.(9分)
∵DB⊥BA,又∵面ABDE⊥面ABC,面ABDE∩面ABC=AB,DB?面ABDE
∴DB⊥面ABC,
∵BD∥AE,
∴EA⊥面ABC.
如图,以C为原点,分别以CA、CB为x、y轴,以过点C与平面垂直的直线为z轴,建立空间直角坐标系,
∵AC=BC=4,
∴各点坐标为:C(0,0,0),A(4,0,0),B(0,4,0)D(0,4,2),E(4,0,4)
∴O(2,0,2),M(2,2,0),设N(a,b,c),
∴
=(a-2,b-2,c),
=(4-a,-b,4-c)(10分)
∵点N在ME上,∴
=λ,即(a-2,b-2,c)=λ(4-a,-b,4-c)
∴
| | a-2=λ(4-a) | | b-2=λ(-b) | | c=λ(4-c) |
| |
?∴
N(,,)(11分)
∵
=(0,0,2)是面ABC的一个法向量,
∴
⊥,∴
=2,解得λ=1.(12分)
∴
=即N是线段EM的中点,
∴当N是EM中点时,ON⊥平面ABDE.(13分)

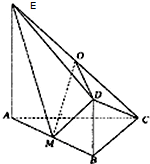 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD= 解:(I)证明:取AC中点F,连接OF、FB(1分)
解:(I)证明:取AC中点F,连接OF、FB(1分)

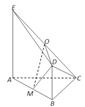 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD= 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=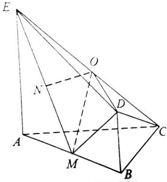 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD= 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=