
【题目】已知抛物线![]() 上的两个动点
上的两个动点![]() ,
, ![]() 的横坐标
的横坐标![]() ,线段
,线段![]() 的中点坐标为
的中点坐标为![]() ,直线
,直线![]() 与线段
与线段![]() 的垂直平分线相交于点
的垂直平分线相交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的面积的最大值.
的面积的最大值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() .
.
【解析】试题分析:(1)根据题设条件可求出线段![]() 的斜率,进而求出线段
的斜率,进而求出线段![]() 的垂直平分线方程,联立直线
的垂直平分线方程,联立直线![]() 与线段
与线段![]() 的垂直平分线方程,即可求出点
的垂直平分线方程,即可求出点![]() 的坐标;(2)联立直线
的坐标;(2)联立直线![]() 与抛物线
与抛物线![]() 的方程,结合韦达定理及弦长公式求出线段
的方程,结合韦达定理及弦长公式求出线段![]() 的长,再求出点
的长,再求出点![]() 到直线
到直线![]() 的距离,即可求出
的距离,即可求出![]() 的表达式,再构造新函数,即可求出最大值.
的表达式,再构造新函数,即可求出最大值.
试题解析:(1)∵![]() ,有
,有![]() ,又点M不在抛物线C上,有
,又点M不在抛物线C上,有![]() ,而
,而![]() ,
, ![]() ,
,
∴线段![]() 的斜率为
的斜率为![]()
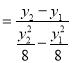
![]()
![]() ,
,
∴线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,即
,即![]() ,
,
由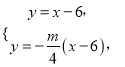 得
得![]() ,
,
即![]() ,得
,得![]() ,
, ![]() ,
,
∴点![]() 的坐标
的坐标![]() .
.
(2)直线![]() 的方程为
的方程为![]() ,
,
由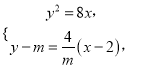 得
得![]() ,
,
∵![]() ,∴
,∴![]() ,结合(1)得
,结合(1)得![]() ,
,
又![]() ,
, ![]() ,
,
∴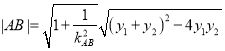
![]()
![]() ,
,
又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]()
![]() ,
,
设![]() ,
, ![]() ,
,
则![]()
![]() ,
,
令![]() 得
得![]() (舍去),
(舍去), ![]() ,
,
由于![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
∴当![]() 时,
时, ![]() 取得最大值,即
取得最大值,即![]() 的面积取得最大值,
的面积取得最大值,
故![]() 的面积的最大值为
的面积的最大值为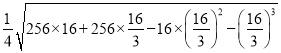
![]() .
.


科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,2017年双11全天交易额达到1682亿元,为规范和评估该行业的情况,相关管理部门制定出针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行评价,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)完成关于商品和服务评价的![]() 列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量![]() :
:
①求对商品和服务全为好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.
附:临界值表:

![]() 的观测值:
的观测值: 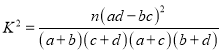 (其中
(其中![]() )
)
关于商品和服务评价的![]() 列联表:
列联表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对任意的n∈N*,有S2n<3Sn,则q的取值范围是( )
A. (0,1] B. (0,2)
C. [1,2) D. (0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为![]() ,且经过点
,且经过点 .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的下顶点为
的下顶点为![]() ,如图所示,点
,如图所示,点![]() 为直线
为直线![]() 上的一个动点,过椭圆
上的一个动点,过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 垂直于
垂直于![]() ,且与
,且与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,四边形
,四边形![]() 和
和![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)

(1)能否由![]() 的把握认为参加书法社团和参加演讲社团有关?
的把握认为参加书法社团和参加演讲社团有关?
(附: 
当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() ,认为事件
,认为事件![]() 与
与![]() 是无关的)
是无关的)
(2)已知既参加书法社团又参加演讲社团的![]() 名同学中,有
名同学中,有![]() 名男同学
名男同学![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 名女同学
名女同学![]() ,
, ![]() ,
, ![]() .现从这
.现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
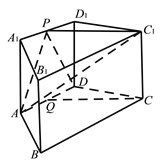
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com