
【题目】已知函数![]() .
.
(1)当![]() 时,证明
时,证明![]() 的图象与
的图象与![]() 轴相切;
轴相切;
(2)当![]() 时,证明
时,证明![]() 存在两个零点.
存在两个零点.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先求导,再设切点,求出切点坐标,即可证明,
(2)分离参数,构造函数,利用导数求出函数的最值,即可证明.
证明:(1)当a=1时,f(x)=(x﹣2)lnx+x﹣1.
∴f′(x)=lnx+![]() +1,
+1,
若f(x)与x轴相切,切点为(x0,0),
∴f(x0)=(x0﹣2)lnx0+x0﹣1=0
f′(x0)=lnx0+![]() +1=0,
+1=0,
解得x0=1或x0=4(舍去)
∴x0=1,
∴切点为(1,0),
故f(x)的图象与x轴相切
(2)∵f(x)=(x﹣2)lnx+ax﹣1=0,
∴a=![]() ﹣
﹣![]() =
=![]() ﹣lnx+
﹣lnx+![]() ,
,
设g(x)=![]() ﹣lnx+
﹣lnx+![]() ,
,
∴g′(x)=﹣![]() ﹣
﹣![]() +
+![]() =
=![]() ,
,
令h(x)=1﹣2x﹣2lnx
易知h(x)在(0,+∞)为减函数,
∵h(1)=1﹣1﹣2ln1=0,
∴当x∈(0,1)时,g′(x)>0,函数g(x)单调递增,
当x∈(1,+∞)时,g′(x)<0,函数g(x)单调递减,
∴g(x)max=g(1)=1,
当x→0时,g(x)→﹣∞,当x→+∞时,g(x)→﹣∞,
∴当a<1时,y=g(x)与y=a有两个交点,
即当a<1时,证明f(x)存在两个零点


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
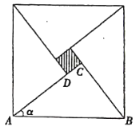
【题目】三国时期吴国的数学家赵爽曾创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个全等的直角三角形与中间的小正方形拼成一个大正方形,其中一个直角三角形中较小的锐角![]() 满足
满足![]() ,现向大正方形内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
,现向大正方形内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且![]() (n∈N*).
(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知等比数列{bn}是递增的,且首项b1和公比q分别是方程(x2﹣4)(x2﹣1)=0实根,求数列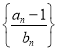 的前n项和为Tn.
的前n项和为Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将n2个数排成n行n列的一个数阵,如图:该数阵第一列的n个数从上到下构成以m为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列(其中m>0).已知a11=2,a13=a61+1,记这n2个数的和为S.下列结论正确的有( )
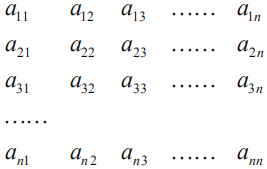
A.m=3B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是圆F1:(x+1)2+y2=16上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)记曲线C与x轴交于A,B两点,M是直线x=1上任意一点,直线MA,MB与曲线C的另一个交点分别为D,E,求证:直线DE过定点H(4,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某部门参加职业技能测试的2000名员工中抽取100名员工,将其成绩(满分100分)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成4组,得到如图所示的频率分布直方图.
分成4组,得到如图所示的频率分布直方图.
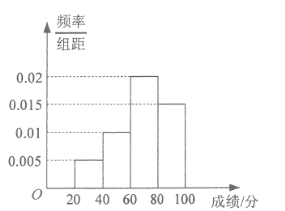
(1)估计该部门参加测试员工的成绩的中位数;
(2)估计该部门参加测试员工的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有6台大型机器,在1个月中,1台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障的概率为![]() .已知1名工人每月只有维修2台机器的能力(若有2台机器同时出现故障,工厂只有1名维修工人,则该工人只能逐台维修,对工厂的正常运行没有任何影响),每台机器不出现故障或出现故障时能及时得到维修,就能使该厂获得10万元的利润,否则将亏损2万元.该工厂每月需支付给每名维修工人1万元的工资.
.已知1名工人每月只有维修2台机器的能力(若有2台机器同时出现故障,工厂只有1名维修工人,则该工人只能逐台维修,对工厂的正常运行没有任何影响),每台机器不出现故障或出现故障时能及时得到维修,就能使该厂获得10万元的利润,否则将亏损2万元.该工厂每月需支付给每名维修工人1万元的工资.
(1)若每台机器在当月不出现故障或出现故障时,有工人进行维修(例如:3台大型机器出现故障,则至少需要2名维修工人),则称工厂能正常运行.若该厂只有1名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有2名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘1名维修工人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com