
| A. | $\frac{{3\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{15}}}{5}$ |
分析 取A1B1中点F,则BF∥EC,∠A1BF是异面直线A1B、EC的夹角,由此能求出异面直线A1B、EC的夹角的余弦值.
解答 解:取A1B1中点F,则BF∥EC,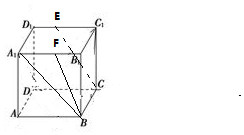
∴∠A1BF是异面直线A1B、EC的夹角,
设正方体ABCD-A1B1C1D1中棱长为2,
则A1F=1,A1B=$\sqrt{4+4}=2\sqrt{2}$,BF=$\sqrt{4+1}=\sqrt{5}$,
∴cos∠A1BF=$\frac{{A}_{1}{B}^{2}+B{F}^{2}-{A}_{1}{F}^{2}}{2{A}_{1}B•BF}$=$\frac{8+5-1}{2×2\sqrt{2}×\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
故选:A.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 36π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
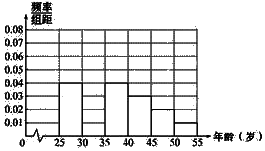 我校高二同学利用暑假进行了社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
我校高二同学利用暑假进行了社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com