
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】图(1)为东方体育中心,其设计方案侧面的外轮廓线如图(2)所示;曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() 且
且![]() 恰好等于圆
恰好等于圆![]() 的半径,
的半径,![]() 与圆相切且
与圆相切且![]() .
.
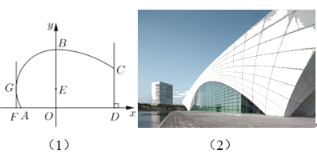
(1)若要求![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)当![]() 时,若要求
时,若要求![]() 不超过45米,求
不超过45米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
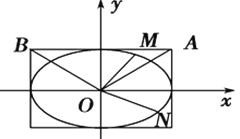
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线方程为![]() ,过其右焦点且斜率不为零的直线
,过其右焦点且斜率不为零的直线![]() 与双曲线交于A,B两点,直线
与双曲线交于A,B两点,直线![]() 的方程为
的方程为![]() ,A,B在直线
,A,B在直线![]() 上的射影分别为C,D.
上的射影分别为C,D.
(1)当![]() 垂直于x轴,
垂直于x轴,![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(2)![]() ,
,![]() 的斜率为正实数,A在第一象限,B在第四象限,试比较
的斜率为正实数,A在第一象限,B在第四象限,试比较![]() 与1的大小;
与1的大小;
(3)是否存在实数![]() ,使得对满足题意的任意
,使得对满足题意的任意![]() ,直线
,直线![]() 和直线
和直线![]() 的交点总在
的交点总在![]() 轴上,若存在,求出所有的
轴上,若存在,求出所有的![]() 值和此时直线
值和此时直线![]() 和
和![]() 交点的位置;若不存在,请说明理由.
交点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在x轴上![]() 分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且
分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且![]() .
.
(1)求椭圆方程;
(2)对于x轴上的某一点T,过T作不与坐标轴平行的直线L交椭圆于![]() 两点,若存在x轴上的点S,使得对符合条件的L恒有
两点,若存在x轴上的点S,使得对符合条件的L恒有![]() 成立,我们称S为T的一个配对点,当T为左焦点时,求T的配对点的坐标;
成立,我们称S为T的一个配对点,当T为左焦点时,求T的配对点的坐标;
(3)在(2)条件下讨论当T在何处时,存在有配对点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com