
【题目】已知数列![]() 满足:
满足:![]() (常数
(常数![]() ),
),![]()
![]() .数列
.数列![]() 满足:
满足:![]()
![]() .
.
(1)求![]()
![]()
![]()
![]() 的值;
的值;
(2)求出数列![]() 的通项公式;
的通项公式;
(3)问:数列![]() 的每一项能否均为整数?若能,求出k的所有可能值;若不能,请说明理由.
的每一项能否均为整数?若能,求出k的所有可能值;若不能,请说明理由.
【答案】(1) ![]()
![]() ;(2)
;(2) ![]() ; (3) k为1,2时数列
; (3) k为1,2时数列![]() 是整数列.
是整数列.
【解析】
(1)经过计算可知:![]() ,由数列
,由数列![]() 满足:
满足:![]() (n=1,2,3,4…),从而可求
(n=1,2,3,4…),从而可求![]()
![]()
![]()
![]() ;
;
(2)由条件可知![]() .得
.得![]() ,两式相减整理得
,两式相减整理得![]() ,从而可求数列
,从而可求数列![]() 的通项公式;
的通项公式;
(3)假设存在正数k,使得数列![]() 的每一项均为整数,则由(2)可知:
的每一项均为整数,则由(2)可知: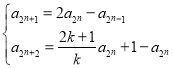 ,由
,由![]() ,
,![]() ,可求得
,可求得![]() .证明
.证明![]() 时,满足题意,说明
时,满足题意,说明![]() 时,数列
时,数列![]() 是整数列.
是整数列.
(1)由已知可知:![]() ,
,
把数列![]() 的项代入
的项代入![]()
求得![]()
![]() ;
;
(2)由![]()
![]()
可知:![]() ①
①
则:![]() ②
②
①②有:![]() ,
,
即:![]()
![]() …
…![]() ,
,![]() …
…![]() ,
,
![]() ;
;
(3)假设存在正数k使得数列![]() 的每一项均为整数,
的每一项均为整数,
则由(2)可知: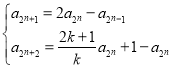 ③,
③,
由![]() ,
,![]() ,可知
,可知![]() ,2.
,2.
当![]() 时,
时,![]() 为整数,利用
为整数,利用![]() 结合③式可知
结合③式可知![]() 的每一项均为整数;
的每一项均为整数;
当![]() 时,③变为
时,③变为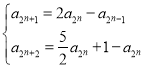 ④
④
用数学归纳法证明![]() 为偶数,
为偶数,![]() 为整数.
为整数.
![]() 时结论显然成立,假设
时结论显然成立,假设![]() 时结论成立,
时结论成立,
这时![]() 为偶数,
为偶数,![]() 为整数,
为整数,
故![]() 为偶数,
为偶数,![]() 为整数,
为整数,
![]() 时,命题成立.
时,命题成立.
故数列![]() 是整数列.
是整数列.
综上所述k为1,2时数列![]() 是整数列.
是整数列.


科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,则称
…,则称![]() 是
是![]() 的“收缩数列”.其中,
的“收缩数列”.其中,![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为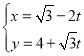 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)设点P为曲线C上的动点,点M,N为直线![]() 上的两个动点,若
上的两个动点,若![]() 是以
是以![]() 为直角的等腰三角形,求
为直角的等腰三角形,求![]() 直角边长的最小值.
直角边长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有l000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族”,计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(Ⅰ)完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该公司员工属于“追光族”与“性别”有关;
的把握认为该公司员工属于“追光族”与“性别”有关;
属于“追光族” | 属于“观望者” | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(Ⅱ)已知被抽取的这l00名员工中有6名是人事部的员工,这6名中有3名属于“追光族”现从这6名中随机抽取3名,求抽取到的3名中恰有1名属于“追光族”的概率.
附: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com