
��M1(0��0)��M2(1��0)����M1ΪԲ�ģ�| M1 M2 | Ϊ�뾶��Բ��x���ڵ�M3 (��ͬ��M2)��������M1����M![]() 2ΪԲ�ģ�| M2 M3 | Ϊ�뾶��Բ��x���ڵ�M4 (��ͬ��M3)������
2ΪԲ�ģ�| M2 M3 | Ϊ�뾶��Բ��x���ڵ�M4 (��ͬ��M3)������
��M2����������MnΪԲ�ģ�| Mn Mn+1 | Ϊ�뾶��Բ��x���ڵ�Mn+2 (��ͬ��Mn+1)��������Mn������
��n��N*ʱ����ԭ������б��Ϊ30���ֱ��![]() ���Mn����An��Bn�����������۶ϣ�
���Mn����An��Bn�����������۶ϣ�
��n��1ʱ��| A1B1 |��2����n��2ʱ��| A2B2 |��![]() ����n��3ʱ��| A3B3 |��
����n��3ʱ��| A3B3 |��![]() ��
��
��n��4ʱ��| A4B4 |��![]() ������
������
�������۶��Ʋ�һ��һ��Ľ��ۣ�����n��N*��| AnBn |�� ![]() ��
��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| m |
| x |
| m |
| 1+x |
| fn(0)-1 |
| fn(0)+2 |
| 4n2+n |
| 4n2+4n+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 3 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•�����һģ����֪ԲO��x2+y2=4��
��2013•�����һģ����֪ԲO��x2+y2=4��| 3 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ��з�����2011�����12�µ��в�����ѧ�������� ���ͣ�044
��h(x)��![]() ��x��[
��x��[![]() ��5]������m�Dz�������ij�����
��5]������m�Dz�������ij�����
(1)д��h(4x)�Ķ�����
(2)��h(x)�ĵ����������䣻
(3)��֪����f(x)(x��[a��b])�����壺f1(x)��min{f(t)|a��t��x}(x��[a��b])��f2(x)��max{f(t)|a��t��x}(x��[a��b])�����У�min{f(x)|x��D}��ʾ����f(x)��D�ϵ���Сֵ��max{f(x)|x��D}��ʾ����f(x)��D�ϵ����ֵ�����磺f(x)��cosx��x��[0����]����f1(x)��cosx��x��[0����]��f2(x)��1��x��[0����]����m��1ʱ����![]() ������ʽt��M1(x)��M2(x)��n���������t��n��ȡֵ��Χ��
������ʽt��M1(x)��M2(x)��n���������t��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013���Ϻ��к�����߿���ѧһģ�Ծ��������Ͼ����������棩 ���ͣ������
 ��ԲO�ཻ��A��B���㣬��|AB|��
��ԲO�ཻ��A��B���㣬��|AB|��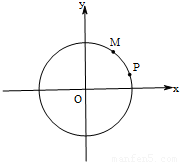
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com