
【题目】平面直角坐标系xOy中,过椭圆M: ![]() =1(a>b>0)焦点的直线x+y﹣2
=1(a>b>0)焦点的直线x+y﹣2 ![]() =0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
=0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
(1)求M的方程;
(2)A、B是M的左、右顶点,C、D是M上的两点,若AC⊥BD,求四边形ABCD面积的最大值.
【答案】
(1)解:设P(x1,y1),Q(x2,y2),G(x0,y0),则 ![]() ,
, ![]() ,
, ![]() ,
,
由此可得 ![]() ,因为x1+x2=2x0,y1+y2=2y0,
,因为x1+x2=2x0,y1+y2=2y0, ![]() ,所以
,所以 ![]() ,
,
又由题意知,M的一个焦点为 ![]() ,故a2﹣b2=8.因此a2=9,b2=1,
,故a2﹣b2=8.因此a2=9,b2=1,
所以M的方程为 ![]() .
.
(2)解:由题意可设直线AC的斜率为,所以直线AC的方程为y=k(x+1),
联立方程组 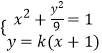 可得,(9+k2)x2+2k2x+k2﹣9=0,所以有
可得,(9+k2)x2+2k2x+k2﹣9=0,所以有 ![]() ,进而可得
,进而可得 ![]() ,所以
,所以 ![]() ,
,
同理可计算出 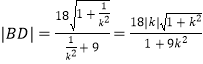 ,
,
所以四边形ABCD面积 ![]() ,
,
设 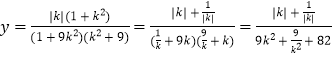 ,令
,令 ![]() (t≥2),所以
(t≥2),所以 ![]() ,此时
,此时 ![]() ,当且仅当
,当且仅当 ![]() 时取得等号,
时取得等号,
所以四边形ABCD面积的最大值为 ![]() .
.
【解析】(1)设P(x1,y1),Q(x2,y2),G(x0,y0),利用平方差法推出 ![]() ,通过M的一个焦点,求出a,b,即可求出M的方程.(2)由题意可设直线AC的斜率为,所以直线AC的方程为y=k(x+1),联立
,通过M的一个焦点,求出a,b,即可求出M的方程.(2)由题意可设直线AC的斜率为,所以直线AC的方程为y=k(x+1),联立 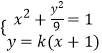 利用韦达定理以及弦长公式,求解四边形ABCD面积的表达式,通过换元法以及基本不等式求解最值即可.
利用韦达定理以及弦长公式,求解四边形ABCD面积的表达式,通过换元法以及基本不等式求解最值即可.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】下列函数中,同时满足两个条件“①x∈R,f( ![]() +X)+f(
+X)+f( ![]() -X)=0;②当﹣
-X)=0;②当﹣ ![]() <x<
<x< ![]() 时,f′(x)>0”的一个函数是( )
时,f′(x)>0”的一个函数是( )
A.f(x)=sin(2x+ ![]() )
)
B.f(x)=cos(2x+ ![]() )
)
C.f(x)=sin(2x﹣ ![]() )
)
D.f(x)=cos(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax﹣1)lnx+ ![]() . (Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线l的方程;
. (Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线l的方程;
(Ⅱ)设函数g(x)=f'(x)有两个极值点x1 , x2 , 其中x1∈(0,e),求g(x1)﹣g(x2)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为 ![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)= ![]() 是奇函数,命题q:函数g(x)=x3﹣x2在区间(0,+∞)上单调递增.则下列命题中为真命题的是( )
是奇函数,命题q:函数g(x)=x3﹣x2在区间(0,+∞)上单调递增.则下列命题中为真命题的是( )
A.p∨q
B.p∧q
C.¬p∧q
D.¬p∨q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设抛物线E:y2=2px(p>0)的焦点为F,准线为直线l,点A、B在直线l上,点M为抛物线E第一象限上的点,△ABM是边长为 ![]() 的等边三角形,直线MF的倾斜角为60°.
的等边三角形,直线MF的倾斜角为60°.
(1)求抛物线E的方程;
(2)如图,直线m过点F交抛物线E于C、D两点,Q(2,0),直线CQ、DQ分别交抛物线E于G、H两点,设直线CD、GH的斜率分别为k1、k2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AD与BC是四面体ABCD中相互垂直的棱,若AD=BC=6,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是( )
A.![]()
B.![]()
C.18
D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记U={1,2,…,100},对数列{an}(n∈N*)和U的子集T,若T=,定义ST=0;若T={t1 , t2 , …,tk},定义ST= ![]() +
+ ![]() +…+
+…+ ![]() .例如:T={1,3,66}时,ST=a1+a3+a66 . 现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.
.例如:T={1,3,66}时,ST=a1+a3+a66 . 现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.
(1)求数列{an}的通项公式;
(2)对任意正整数k(1≤k≤100),若T{1,2,…,k},求证:ST<ak+1;
(3)设CU,DU,SC≥SD , 求证:SC+SC∩D≥2SD .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com