
【题目】已知![]() 是平面内凸三十五边形的35个顶点,且
是平面内凸三十五边形的35个顶点,且![]() 中任何两点之间的距离不小于
中任何两点之间的距离不小于![]() . 证明:从这35个点中可以选出五个点,使得这五个点中任意两点之间的距离不小于3.
. 证明:从这35个点中可以选出五个点,使得这五个点中任意两点之间的距离不小于3.
【答案】见解析
【解析】
先证明一个引理
引理 设![]() 为
为![]() 这35个点中的任意一点.则在余下的34个点中,至多六个点与点
这35个点中的任意一点.则在余下的34个点中,至多六个点与点![]() 的距离小于3.
的距离小于3.
证明 用反证法.
如图,假设有7个点(不妨设为![]() )与点
)与点![]() 的距离小于3.
的距离小于3.

由题设知![]() .
.
故 ![]() 这六个角中至少有一个角不大于
这六个角中至少有一个角不大于![]() (不妨设
(不妨设![]() ).
).
设![]() ,
,![]() .则
.则![]() .
.
根据对称性不妨设![]() .
.
由于![]() ,因此,
,因此,![]()
在区间![]() )上为增函数.
)上为增函数.
故![]() .
.
从而![]() ,与条件矛盾.
,与条件矛盾.
回到原题.
根据引理,从点![]() 出发的34条线段
出发的34条线段![]() 中至多有6条线段的长度小于3,即至少有28条线段的长度不小于3.不妨设线段
中至多有6条线段的长度小于3,即至少有28条线段的长度不小于3.不妨设线段![]() 的长度不小于3.
的长度不小于3.
再考虑从点![]() 出发的27条线段
出发的27条线段![]() .同理,至少有21条线段的长度不小于3.不妨设线段
.同理,至少有21条线段的长度不小于3.不妨设线段![]() 的长度不小于3.
的长度不小于3.
再考虑从点![]() 出发的20条线段
出发的20条线段![]() .同理,至少有14条线段的长度不小于3.不妨设线段
.同理,至少有14条线段的长度不小于3.不妨设线段![]() 的长度不小于3.
的长度不小于3.
再考虑从点![]() 出发的13条线段
出发的13条线段![]() .同理,至少有7条线段的长度不小于3.不妨设线段
.同理,至少有7条线段的长度不小于3.不妨设线段![]() 的长度不小于3.
的长度不小于3.
这样得到五个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,其中任意两点之间的距离不小于3.
,其中任意两点之间的距离不小于3.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再把图象上所有点的横坐标缩短到原来的
个单位,再把图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图象,则关于
的图象,则关于![]() 的图象,下列结论不正确的是
的图象,下列结论不正确的是
A. 周期为![]() B. 关于点
B. 关于点![]() 对称
对称
C. 在![]() 单调递增 D. 在
单调递增 D. 在![]() 单调递减
单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,在高三年级中随机选取![]() 名学生进行跟踪问卷,其中每周线上学习数学时间不少于
名学生进行跟踪问卷,其中每周线上学习数学时间不少于![]() 小时的有
小时的有![]() 人,在这
人,在这![]() 人中分数不足
人中分数不足![]() 分的有
分的有![]() 人;在每周线上学习数学时间不足于
人;在每周线上学习数学时间不足于![]() 小时的人中,在检测考试中数学平均成绩不足
小时的人中,在检测考试中数学平均成绩不足![]() 分的占
分的占![]() .
.
(1)请完成![]() 列联表;并判断是否有
列联表;并判断是否有![]() 的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
分数不少于 | 分数不足 | 合计 | |
线上学习时间不少于 | |||
线上学习时间不足 | |||
合计 |
(2)在上述样本中从分数不足于![]() 分的学生中,按照分层抽样的方法,抽到线上学习时间不少于
分的学生中,按照分层抽样的方法,抽到线上学习时间不少于![]() 小时和线上学习时间不足
小时和线上学习时间不足![]() 小时的学生共
小时的学生共![]() 名,若在这
名,若在这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求这
人,求这![]() 人每周线上学习时间都不足
人每周线上学习时间都不足![]() 小时的概率.(临界值表仅供参考)
小时的概率.(临界值表仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式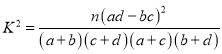 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拿破仑为人好学,是法兰西科学院院士,他对数学方面很感兴趣,在行军打仗的空闲时间,经常研究平面几何。他提出了著名的拿破仑定理:以三角形各边为边分别向外(内)侧作等边三角形,则它们的中心构成一个等边三角形。如图所示,以等边![]() 的三条边为边,向外作
的三条边为边,向外作![]() 个正三角形,取它们的中心
个正三角形,取它们的中心![]() ,顺次连接,得到
,顺次连接,得到![]() ,图中阴影部分为
,图中阴影部分为![]() 与
与![]() 的公共部分。若往
的公共部分。若往![]() 中投掷一点,则该点落在阴影部分内的概率为( )
中投掷一点,则该点落在阴影部分内的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.

(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 与圆
与圆![]() 相交的弦长等于椭圆
相交的弦长等于椭圆![]() :
: ![]() (
(![]() )的焦距长.
)的焦距长.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,椭圆
为原点,椭圆![]() 与抛物线
与抛物线![]() (
(![]() )交于
)交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
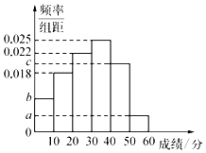
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: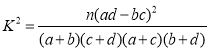 ,其中
,其中![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设双曲线![]() 的上焦点为
的上焦点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为双曲线虚轴的左端点,已知
为双曲线虚轴的左端点,已知![]() 的离心率为
的离心率为![]() ,且
,且![]() 的面积
的面积![]() .
.

(1)求双曲线![]() 的方程;
的方程;
(2)设抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() ,动直线
,动直线![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的准线相交于点
的准线相交于点![]() ,试推断以线段
,试推断以线段![]() 为直径的圆是否恒经过
为直径的圆是否恒经过![]() 轴上的某个定点
轴上的某个定点![]() ?若是,求出定点
?若是,求出定点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com