
已知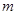 、
、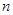 是两条不同的直线,
是两条不同的直线,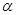 、
、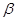 是两个不同的平面,则下面命题中正确的是( )
是两个不同的平面,则下面命题中正确的是( )
A、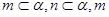 ∥
∥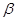 ,
,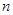 ∥
∥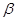
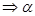 ∥
∥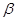
B、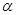 ∥
∥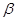
 ,
,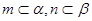
 ∥
∥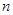
C、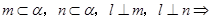
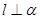
D、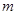 ∥
∥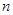 ,
,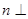
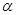

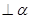
科目:高中数学 来源: 题型:
(1)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(2)对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;
(3)在AB上是否存在两个不同的点D′,E′,使沿折线.PD′E′O修建公路的总造价小于(2)中得到的最小总造价?证明你的结论.

a)
第19题图
(文)如图b所示,直四棱柱ABCD-A1B1C1D1中,∠ADC=90°,△ABC为等边三角形,且AA1=AD=DC=2.
(1)求AC1与BC所成角的余弦值;
(2)求二面角C1-BD-C的大小;
(3)设M是BD上的点,当DM为何值时,D1M⊥平面A1C1D?并证明你的结论.

第19题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com