
直线 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、 既不充分也不必要条件
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:甘肃省天水一中2011-2012学年高二第二学段测试数学文科试题 题型:013
下列说法中,正确的是
A.命题“若a<b,则am2<bm2”的否命题是假命题.
B.设α,β为两个不同的平面,直线![]() ,则“l⊥β”是“α⊥β”成立的充分不必要条件.
,则“l⊥β”是“α⊥β”成立的充分不必要条件.
C.命题“![]() ”的否定是“
”的否定是“![]() ”.
”.
D.已知x∈R,则“x>1”是“x>2”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北荆州、黄冈、襄阳、十堰、宜昌、孝感、恩施七市高三4月联考文数学卷(解析版) 题型:选择题
已知a,β表示两个不同的平面,l为a内的一条直线,则“a//β是“l//β”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:专项题 题型:单选题
查看答案和解析>>
科目:高中数学 来源:黑龙江省模拟题 题型:单选题
 ,则“l⊥β”是“α⊥β”成立的充分不必要条件
,则“l⊥β”是“α⊥β”成立的充分不必要条件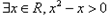 ”的否定是“
”的否定是“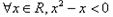 ”
”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com