
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{4}$+$\frac{1}{4}$i | D. | $\frac{\sqrt{3}}{4}$-$\frac{1}{4}$i |
分析 直接利用复数代数形式的乘除运算化简复数z,求出$\overline{z}$,代入z•$\overline{z}$计算得答案.
解答 解:∵z=$\frac{\sqrt{3}+i}{(1-\sqrt{3}i)^{2}}$=$\frac{\sqrt{3}+i}{-2-2\sqrt{3}i}=\frac{(\sqrt{3}+i)(-2+2\sqrt{3}i)}{(-2-2\sqrt{3}i)(-2+2\sqrt{3}i)}$=$\frac{-4\sqrt{3}+4i}{16}=-\frac{\sqrt{3}}{4}+\frac{1}{4}i$,
∴$\overline{z}=-\frac{\sqrt{3}}{4}-\frac{1}{4}i$.
则z•$\overline{z}$=$(-\frac{\sqrt{3}}{4}+\frac{1}{4}i)•(-\frac{\sqrt{3}}{4}-\frac{1}{4}i)=\frac{1}{4}$.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


科目:高中数学 来源: 题型:解答题
| 患呼吸系统疾病 | 未患呼吸系统疾病 | 总计 | |
| 重污染地区 | 103 | 1 397 | 1 500 |
| 轻污染地区 | 13 | 1 487 | 1 500 |
| 总计 | 116 | 2 884 | 3 000 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充分必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 (a>b>0)的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率e=$\frac{\sqrt{3}}{2}$,△DEF2的面积为1-$\frac{\sqrt{3}}{2}$.若M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知OP⊥OQ.
如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 (a>b>0)的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率e=$\frac{\sqrt{3}}{2}$,△DEF2的面积为1-$\frac{\sqrt{3}}{2}$.若M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知OP⊥OQ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
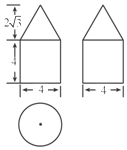 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的体积为( )
如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的体积为( )| A. | 16π+$\sqrt{3}π$ | B. | 16π+8$\sqrt{3}$π | C. | 16π+$\frac{8}{3}\sqrt{3}π$ | D. | 16π+$\frac{4}{3}\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,E,E,G,H分别是棱AB,BB1,BC,CC1的中点,∠ABC=90°.则异面直线EF和GH所成的角是( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,E,E,G,H分别是棱AB,BB1,BC,CC1的中点,∠ABC=90°.则异面直线EF和GH所成的角是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com