练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行如图所示的程序框图，则输出的k的值为（ ）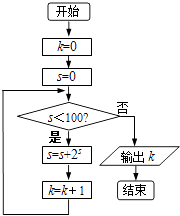

    A.7
    B.6
    C.5
    D.4

    【答案】D
    【解析】解：分析程序中各变量、各语句的作用，
    再根据流程图所示的顺序，
    可知：该程序的作用是：
    输出不满足条件S=0+1+2+8+…＜100时，k+1的值．
    第一次运行：满足条件，s=1，k=1；
    第二次运行：满足条件，s=3，k=2；
    第三次运行：满足条件，s=11＜100，k=3；满足判断框的条件，继续运行，
    第四次运行：s=1+2+8+211＞100，k=4，不满足判断框的条件，退出循环．
    故最后输出k的值为4．
    故选：D．
    分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是输出输出不满足条件S=0+1+2+8+…＜100时，k+1的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的左右焦点分别为F1 ， F2 ， 且F2为抛物线 的焦点，C2的准线l被C1和圆x2+y2=a2截得的弦长分别为 和4．
    （1）求C1和C2的方程；
    （2）直线l1过F1且与C2不相交，直线l2过F2且与l1平行，若l1交C1于A，B，l2交C1交于C，D，且在x轴上方，求四边形AF1F2C的面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x米，圆心角为θ（弧度）．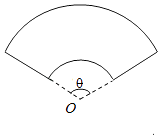
    （1）求θ关于x的函数关系式；
    （2）已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用之比为y，求y关于x的函数关系式，并求出y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项数列{an}满足a1=1，（n+1）a2n+1+an+1an﹣na =0，数列{bn}的前n项和为Sn且Sn=1﹣bn ．
    （1）求{an}和{bn}的通项；
    （2）令cn= ， ①求{cn}的前n项和Tn；
    ②是否存在正整数m满足m＞3，c2 ， c3 ， cm成等差数列？若存在，请求出m；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC﹣A1B1C1中，CA=CB，M，N，P分别为AB，A1C1 ， BC的中点．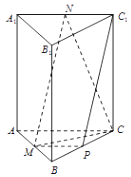
    求证：
    （1）C1P∥平面MNC；
    （2）平面MNC⊥平面ABB1A1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新课标要求学生数学模块学分认定由模块成绩决定，模块成绩由模块考试成绩和平时成绩构成，各占50%，若模块成绩大于或等于60分，获得2学分，否则不能获得学分（为0分），设计一算法，通过考试成绩和平时成绩计算学分，并画出程序框图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点M（﹣2，0），N（2，0），动点P满足条件 ．记动点P的轨迹为W．
    （1）求W的方程；
    （2）若A，B是W上的不同两点，O是坐标原点，求 的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和为Sn ， 且Sn=n（n+1）（n∈N*）
    （1）求数列{an}的通项公式；
    （2）若数列{bn}满足：an= + + +…+ ，求数列{bn}的通项公式；
    （3）令cn= （n∈N*），求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明准备利用暑假时间去旅游，妈妈为小明提供四个景点，九寨沟、泰山、长白山、武夷山．小明决定用所学的数学知识制定一个方案来决定去哪个景点：（如图）曲线 和直线 交于点 ．以 为起点，再从曲线 上任取两个点分别为终点得到两个向量，记这两个向量的数量积为 ．若 去九寨沟；若 去泰山；若 去长白山； 去武夷山．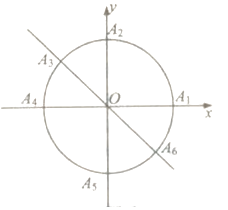

    （1）若从 这六个点中任取两个点分别为终点得到两个向量，分别求小明去九寨沟的概率和不去泰山的概率；
    （2）按上述方案，小明在曲线 上取点 作为向量的终点，则小明决定去武夷山．点 在曲线 上运动，若点 的坐标为 ，求 的最大值．

    查看答案和解析>>

    同步练习册答案