
ЁОЬтФПЁПОнФГЦјЯѓжааФЙлВьКЭдЄВтЃКЗЂЩњгкMЕиЕФЩГГОБЉвЛжБЯђе§ФЯЗНЯђвЦЖЏЃЌЦфвЦЖЏЫйЖШv(km/h)гыЪБМфt(h)ЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎЙ§ЯпЖЮOCЩЯвЛЕуT(t,0)зїКсжсЕФДЙЯпlЃЌЬнаЮOABCдкжБЯпlзѓВрВПЗжЕФУцЛ§МДЪБМфt(h)ФкЩГГОБЉЫљОЙ§ЕФТЗГЬs(km)ЃЎ

(1)ЕБtЃН4ЪБЃЌЧѓsЕФжЕЃЛ
(2)НЋsЫцtБфЛЏЕФЙцТЩгУЪ§бЇЙиЯЕЪНБэЪОГіРДЃЛ
(3)ШєNГЧЮЛгкMЕие§ФЯЗНЯђЃЌЧвОрMЕи650 kmЃЌЪдХаЖЯетГЁЩГГОБЉЪЧЗёЛсЧжЯЎЕНNГЧЃЌШчЙћЛсЃЌдкЩГГОБЉЗЂЩњКѓЖрГЄЪБМфЫќНЋЧжЯЎЕНNГЧЃПШчЙћВЛЛсЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ24ЃЛЃЈ2ЃЉ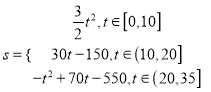 ЃЛЃЈ3ЃЉЩГГОБЉЗЂЩњ30 hКѓНЋЧжЯЎЕНNГЧЃЎ
ЃЛЃЈ3ЃЉЩГГОБЉЗЂЩњ30 hКѓНЋЧжЯЎЕНNГЧЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіЯпЖЮOAЕФНтЮіЪНЮЊv=4tЃЌШЛКѓАбt=10жБНгДњШыЧѓГіДЫЪБЕФЫйЖШЃЌМДПЩЧѓГіSЃЈtЃЉЕФжЕЃЛЃЈ2ЃЉЯШЗжЖЮЧѓГіЫйЖШvгыЪБМфtЕФКЏЪ§КЏЪ§ЙиЯЕЃЌдйЗжБ№ГЫвдЪБМфМДПЩЧѓЕУЖдгІЕФКЏЪ§SЃЈtЃЉЕФНтЮіЪНЃЛЃЈ3ЃЉЯШгЩЗжЖЮКЏЪ§ЕФНтЮіЪНвдМАЖдгІЕФЖЈвхгђПЩвдЧѓЕУЦфзюДѓжЕЃЌЗЂЯжЦфзюДѓжЕДѓгк650ЃЌМДПЩЯТНсТлЛсЧжЯЎЕНNГЧЃЌдйАбSЃЈtЃЉ=650ДњШыМДПЩЧѓГіЖдгІЕФtЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉгЩЭМЯёПЩжЊЃЌЕБtЃН4ЪБЃЌvЃН3ЁС4ЃН12ЃЌ
ЫљвдSЃН![]() ЁС4ЁС12ЃН24 kmЃЎ
ЁС4ЁС12ЃН24 kmЃЎ
ЃЈ2ЃЉЕБ0ЁмtЁм10ЪБЃЌSЃН![]() ЁЄtЁЄ3tЃН
ЁЄtЁЄ3tЃН![]() ЃЛ
ЃЛ
ЕБ10<tЁм20ЪБЃЌSЃН![]() ЁС10ЁС30ЃЋ30ЃЈtЃ10ЃЉЃН30tЃ150ЃЛ
ЁС10ЁС30ЃЋ30ЃЈtЃ10ЃЉЃН30tЃ150ЃЛ
ЕБ20<tЁм35ЪБЃЌSЃН![]() ЁС10ЁС30ЃЋ10ЁС30ЃЋЃЈtЃ20ЃЉЁС30Ѓ
ЁС10ЁС30ЃЋ10ЁС30ЃЋЃЈtЃ20ЃЉЁС30Ѓ![]() ЁСЃЈtЃ20ЃЉЁС2ЃЈtЃ20ЃЉЃН
ЁСЃЈtЃ20ЃЉЁС2ЃЈtЃ20ЃЉЃН![]() ЃЎ
ЃЎ
злЩЯПЩжЊЃЌ 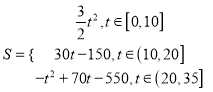 ЃЎ
ЃЎ
ЃЈ3ЃЉвђЮЊЕБtЁЪ[0ЃЌ10]ЪБЃЌSmaxЃН![]() ЁС102ЃН150<650ЃЌ
ЁС102ЃН150<650ЃЌ
ЕБtЁЪЃЈ10ЃЌ20]ЪБЃЌSmaxЃН30ЁС20Ѓ150ЃН450<650ЃЌ
ЫљвдЕБtЁЪЃЈ20ЃЌ35]ЪБЃЌСю![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎвђЮЊ20<tЁм35ЃЌЫљвдtЃН30ЃЎ
ЃЎвђЮЊ20<tЁм35ЃЌЫљвдtЃН30ЃЎ
ЙЪЩГГОБЉЗЂЩњ30 hКѓНЋЧжЯЎЕНNГЧЃЎ


 ЪБПЬзМБИзХЪюМйзївЕдзгФмГіАцЩчЯЕСаД№АИ
ЪБПЬзМБИзХЪюМйзївЕдзгФмГіАцЩчЯЕСаД№АИ ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018Фъ1дЛ8ШеЃЌжаЙВжабыЁЂЙњЮёдКТЁжиОйааЙњМвПЦбЇММЪѕНБРјДѓЛсЃЌдкПЦММНчв§ЗЂШШСвЗДЯьЃЌзджїДДаТе§ГЩЮЊв§СьОМУЩчЛсЗЂеЙЕФЧПОЂЖЏСІ.ФГПЦбаЕЅЮЛдкбаЗЂаТВњЦЗЕФЙ§ГЬжаЗЂЯжСЫвЛжжаТВФСЯЃЌгЩДѓЪ§ОнВтЕУИУВњЦЗЕФадФмжИБъжЕ![]() гыетжжаТВФСЯЕФКЌСП
гыетжжаТВФСЯЕФКЌСП![]() ЃЈЕЅЮЛЃКПЫЃЉЕФЙиЯЕЮЊЃКЕБ
ЃЈЕЅЮЛЃКПЫЃЉЕФЙиЯЕЮЊЃКЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЪЧ
ЪЧ![]() ЕФЖўДЮКЏЪ§ЃЛЕБ
ЕФЖўДЮКЏЪ§ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() .ВтЕУЪ§ОнШчБэЃЈВПЗжЃЉ
.ВтЕУЪ§ОнШчБэЃЈВПЗжЃЉ
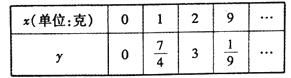
ЃЈ1ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪН
ЕФКЏЪ§ЙиЯЕЪН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЦфКЏЪ§![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() МАКЏЪ§
МАКЏЪ§![]() ЃЈaЃЌbЃЌcЁЪRЃЉЃЌШєa>b>cЧвa+b+c=0.
ЃЈaЃЌbЃЌcЁЪRЃЉЃЌШєa>b>cЧвa+b+c=0.
ЃЈ1ЃЉжЄУїЃКf(x)ЕФЭМЯёгыg(x)ЕФЭМЯёвЛЖЈгаСНИіНЛЕуЃЛ
ЃЈ2ЃЉЧыгУЗДжЄЗЈжЄУїЃК![]() ЃЛ
ЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЮЊЦцКЏЪ§ЃЌЧвЯрСкСНЖдГЦжсМфЕФОрРыЮЊ
ЃЉЮЊЦцКЏЪ§ЃЌЧвЯрСкСНЖдГЦжсМфЕФОрРыЮЊ![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФЕЅЕїЕнМѕЧјМфЃЛ
ЕФЕЅЕїЕнМѕЧјМфЃЛ
ЃЈ2ЃЉНЋКЏЪ§![]() ЕФЭМЯѓби
ЕФЭМЯѓби![]() жсЗНЯђЯђгвЦНвЦ
жсЗНЯђЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйАбКсзјБъЫѕЖЬЕНдРДЕФ
ИіЕЅЮЛГЄЖШЃЌдйАбКсзјБъЫѕЖЬЕНдРДЕФ![]() ЃЈзнзјБъВЛБфЃЉЃЌЕУЕНКЏЪ§
ЃЈзнзјБъВЛБфЃЉЃЌЕУЕНКЏЪ§![]() ЕФЭМЯѓ.ЕБ
ЕФЭМЯѓ.ЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФжЕгђ.
ЕФжЕгђ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=|aЉ3x|Љ|2+x|ЃЎ
ЃЈ1ЃЉШєa=2ЃЌНтВЛЕШЪНfЃЈxЃЉЁм3ЃЛ
ЃЈ2ЃЉШєДцдкЪЕЪ§aЃЌЪЙЕУВЛЕШЪНfЃЈxЃЉЁн1Љa+2|2+x|ГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдІСЁЪRЃЌnЁЪ[0ЃЌ2]ЃЌЯђСП ![]() =ЃЈ2n+3cosІСЃЌnЉ3sinІСЃЉЕФГЄЖШВЛГЌЙ§6ЕФИХТЪЮЊЃЈ ЃЉ
=ЃЈ2n+3cosІСЃЌnЉ3sinІСЃЉЕФГЄЖШВЛГЌЙ§6ЕФИХТЪЮЊЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМйЩшЙигкФГЩшБИЕФЪЙгУФъЯо![]() ЃЈФъЃЉКЭЫљжЇГіЕФЮЌаоЗбгУ
ЃЈФъЃЉКЭЫљжЇГіЕФЮЌаоЗбгУ![]() ЃЈЭђдЊЃЉгаШчЯТЭГМЦзЪСЯЃК
ЃЈЭђдЊЃЉгаШчЯТЭГМЦзЪСЯЃК
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
ШєгЩзЪСЯжЊЃЌ ![]() Жд
Жд![]() ГЪЯпадЯрЙиЙиЯЕЃЌЪдЧѓЃК
ГЪЯпадЯрЙиЙиЯЕЃЌЪдЧѓЃК
ЃЈ1ЃЉЛиЙщжБЯпЗНГЬЃЛ
ЃЈ2ЃЉЙРМЦЪЙгУФъЯоЮЊ10ФъЪБЃЌЮЌаоЗбгУдМЪЧЖрЩйЃП
ВЮПМЙЋЪНЃКЛиЙщжБЯпЗНГЬЃК ![]() .Цфжа
.Цфжа
ЃЈзЂЃК ![]() )
)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=ax+bx-cxЃЌЦфжаcЃОaЃО0ЃЌcЃОbЃО0ЃЎШєaЃЌbЃЌcЪЧЁїABCЕФШ§ЬѕБпГЄЃЌдђЯТСаНсТле§ШЗЕФЪЧ______ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
ЂйЖдШЮвтЕФxЁЪЃЈ-ЁоЃЌ1ЃЉЃЌЖМгаfЃЈxЃЉЃО0ЃЛ
ЂкДцдкxЁЪRЃЌЪЙaxЃЌbxЃЌcxВЛФмЙЙГЩвЛИіШ§НЧаЮЕФШ§ЬѕБпГЄЃЛ
ЂлШєЁїABCЪЧЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮЃЌдђДцдкxЁЪЃЈ1ЃЌ2ЃЉЃЌЪЙfЃЈxЃЉ=0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШє![]() ,ЧѓЧњЯп
,ЧѓЧњЯп![]() дк
дк![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШє![]() дк
дк![]() ЩЯЕЅЕїЕнді,ЧѓЪЕЪ§
ЩЯЕЅЕїЕнді,ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБ![]() ЪБ,ЧѓжЄ:ЖдгкШЮвтЕФ
ЪБ,ЧѓжЄ:ЖдгкШЮвтЕФ![]()
![]() ,Ољга
,Ољга![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com