
【题目】(2017吉林延边州模拟)已知在△ABC中,B(-1,0),C(1,0),且|AB|+|AC|=4.
(1)求动点A的轨迹M的方程;
(2)P为轨迹M上的动点,△PBC的外接圆为☉O1,当点P在轨迹M上运动时,求点O1到x轴的距离的最小值.
【答案】(1)![]() =1(y≠0);(2)
=1(y≠0);(2)![]() .
.
【解析】试题分析:
(1)分析题意可得动点A的轨迹是以B,C为焦点,长轴长为4的椭圆,然后求出![]() 后可得椭圆的方程.(2)设P(x0,y0),可求得线段PB的垂直平分线方程,然后与线段BC的垂直平分线方程联立后可得两直线的交点的纵坐标,此交点的纵坐标的绝对值即为点O1到x轴的距离.然后根据根据函数的单调性可得所求的最值.
后可得椭圆的方程.(2)设P(x0,y0),可求得线段PB的垂直平分线方程,然后与线段BC的垂直平分线方程联立后可得两直线的交点的纵坐标,此交点的纵坐标的绝对值即为点O1到x轴的距离.然后根据根据函数的单调性可得所求的最值.
试题解析:
(1)根据题意知![]() ,
,
∴动点A的轨迹是以B,C为焦点,长轴长为4的椭圆,不包括椭圆与x轴的交点.
设椭圆的方程为![]() =1(a>b>0且y≠0),
=1(a>b>0且y≠0),
则2c=2,2a=4,
∴a=2,c=1,
∴b=![]() .
.
∴动点A的轨迹M的方程为![]() =1(y≠0).
=1(y≠0).
(2)设P(x0,y0),不妨设0<y0≤![]() ,
,
则线段PB的垂直平分线方程为y![]() =-
=-![]() ,
,
线段BC的垂直平分线方程为x=0,
两条垂线方程联立求得y=![]() .
.
∵![]() =1,
=1,
∴y=![]() .
.
∴☉O1的圆心O1到x轴的距离为d=![]() .
.
又函数![]() 在区间(0,
在区间(0,![]() 内单调递减,
内单调递减,
∴当y0=![]() 时,
时,![]() 有最小值,且ymin=
有最小值,且ymin=![]() .
.
∴点O1到x轴的距离的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 相交于
相交于![]() ,
, ![]() 两点,分别以点
两点,分别以点![]() ,
, ![]() 为切点作圆
为切点作圆![]() 的切线.若切线恰好都经过抛物线
的切线.若切线恰好都经过抛物线![]() 的焦点
的焦点![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】由题得设A![]() ,
, ![]() ,联立圆E和抛物线得:
,联立圆E和抛物线得: ![]() ,代入点A得
,代入点A得![]() ,又AF为圆的切线,故
,又AF为圆的切线,故![]() ,由抛物线得定义可知:AF=
,由抛物线得定义可知:AF=![]() ,故
,故![]() 化简得:
化简得: ![]() ,将点A代入圆得:
,将点A代入圆得: ![]()
![]()
![]() ,而
,而![]() =
=![]() ,故
,故![]() 故选A
故选A
点睛:此题几何关系较为复杂,我们根据问题可知借此题关键为找到p和r的关系,我们可根据圆和抛物线相交结合抛物线的焦点弦长结论综合计算可得其关系,从而求解
【题型】单选题
【结束】
12
【题目】已知函数![]() 在点
在点![]()
![]() 处的切线为
处的切线为![]() ,若直线
,若直线![]() 在
在![]() 轴上的截距恒小于
轴上的截距恒小于![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图3,![]() 是一个直角梯形,
是一个直角梯形,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,
,![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() 、
、![]() ,得到如图4所示的四棱锥
,得到如图4所示的四棱锥![]() .
.
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求直线![]() 与面
与面![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).
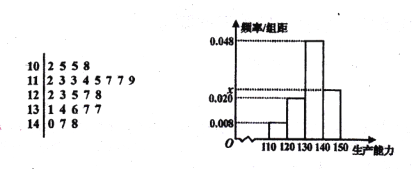
(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购。为拓展市场,某调研组对甲、乙两个品牌的共享单车在5个城市的用户人数进行统计,得到如下数据:
城市 品牌 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(百万) | 4 | 3 | 8 | 6 | 12 |
乙品牌(百万) | 5 | 7 | 9 | 4 | 3 |
(Ⅰ)如果共享单车用户人数超过5百万的城市称为“优质潜力城市”,否则“非优”,请据此判断是否有85%的把握认为“优质潜力城市”与共享单车品牌有关?
(Ⅱ)如果不考虑其它因素,为拓展市场,甲品牌要从这5个城市中选出3个城市进行大规模宣传.
①在城市Ⅰ被选中的条件下,求城市Ⅱ也被选中的概率;
②以![]() 表示选中的城市中用户人数超过5百万的个数,求随机变量
表示选中的城市中用户人数超过5百万的个数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: K2=![]() ,n=a+b+c+d
,n=a+b+c+d
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+bx+c)ex(a>0)的导函数y=f′(x)的两个零点为-3和0.
(1)求f(x)的单调区间;
(2)若f(x)的极小值为-1,求f(x)的极大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com