
【题目】过椭圆W:![]() 的左焦点
的左焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,其中
两点,其中![]()
![]() ,另一条过
,另一条过![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点(不与
两点(不与![]() 重合),且
重合),且![]() 点不与点
点不与点![]() 重合.过
重合.过![]() 作
作![]() 轴的垂线分别交直线
轴的垂线分别交直线![]() ,
,![]() 于
于![]() ,
,![]() .
.
(Ⅰ)求![]() 点坐标和直线
点坐标和直线![]() 的方程;
的方程;
(Ⅱ)求证:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的![]() 个小球,其中有红色球
个小球,其中有红色球![]() 个,编号分别为
个,编号分别为![]() ;白色球
;白色球![]() 个, 编号分别为
个, 编号分别为![]() , 从盒子中任取
, 从盒子中任取![]() 个小球(假设取到任何—个小球的可能性相同).
个小球(假设取到任何—个小球的可能性相同).
(1)求取出的![]() 个小球中,含有编号为
个小球中,含有编号为![]() 的小球的概率;
的小球的概率;
(2)在取出的![]() 个小球中, 小球编号的最大值设为
个小球中, 小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
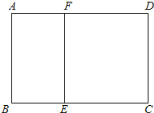
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
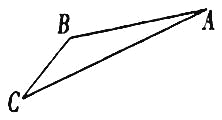
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 点为圆
点为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2x和g(x)=2x的图象如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.

(1)请指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,判断![]() 与
与![]() ,f(2 019)与g(2 019)的大小.
,f(2 019)与g(2 019)的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com